题目内容
已知抛物线y=x2﹣(k+2)x+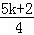 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
(1)求证:无论k取何实数值,抛物线总与x轴有两个不同的交点;
(2)抛物线于x轴交于点A、B,直线与x轴交于点C,设A、B、C三点的横坐标分别是x1、x2、x3,求x1•x2•x3的最大值;
(3)如果抛物线与x轴的交点A、B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D、E,直线AD交直线CE于点G(如图),且CA•GE=CG•AB,求抛物线的解析式.

(1)证明:∵△=(k+2)2﹣4×1× =k2﹣k+2=(k﹣)2+,
=k2﹣k+2=(k﹣)2+,
∵(k﹣)2≥0,
∴△>0,
∴无论k取何实数值,抛物线总与x轴有两个不同的交点;
(2)解:∵抛物线于x轴交于点A、B,直线与x轴交于点C,设A、B、C三点的横坐标分别是x1、x2、x3,
∴x1•x2= ,
,
令0=(k+1)x+(k+1)2,
解得:x=﹣(k+1),
即x3=﹣(k+1),
∴x1•x2•x3=﹣(k+1)• =﹣(k+
=﹣(k+ )2+
)2+ ,
,
∴x1•x2•x3的最大值为: ;
;
(3)解:∵CA•GE=CG•AB,
∴ ,
,
∵∠ACG=∠BCE,
∴△CAG∽△CBE,
∴∠CAG=∠CBE,
∵∠AOD=∠BOE,
∴△OAD∽△OBE,
∴ ,
,
∵抛物线与x轴的交点A、B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D、E,
∴OA•OB= ,OD=
,OD= ,OE=(k+1)2,
,OE=(k+1)2,
∴OA•OB=OD,
∴ ,
,
∴OB2=OE,
∴OB=k+1,
∴点B(k+1,0),
将点B代入抛物线y=x2﹣(k+2)x+ 得:(k+1)2﹣(k+2)(k+1)﹣
得:(k+1)2﹣(k+2)(k+1)﹣ =0,
=0,
解得:k=2,
∴抛物线的解析式为:y=x2﹣4x+3.

我市通过网络投票选出了一批“最有孝心的美少年”.根据各县市区的入选结果制作出如下统计表,后来发现,统计表中前三行的所有数据都是正确的,后三行中有一个数据是错误的.请回答下列问题:
(1)统计表中a= 0.1 ,b= 6 ;
(2)统计表后三行中哪一个数据是错误的?该数据的正确值是多少?
(3)株洲市决定从来自炎陵县的4位“最有孝心的美少年”中,任选两位作为市级形象代言人.A、B是炎陵县“最有孝心的美少年”中的两位,问A、B同时入选的概率是多少?
| 区域 | 频数 | 频率 |
| 炎陵县 | 4 | a |
| 茶陵县 | 5 | 0.125 |
| 攸县 | b | 0.15 |
| 醴陵市 | 8 | 0.2 |
| 株洲县 | 5 | 0.125 |
| 株洲市城区 | 12 | 0.25 |
某几何体的主视图、左视图和俯视图分别如图,则该几何体的体积为( )
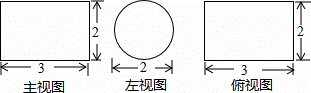
|
| A. | 3π | B. | 2π | C. | π | D. | 12 |
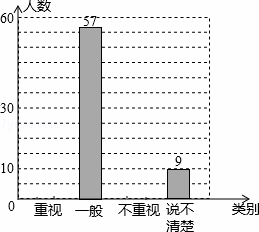
某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表
| 类别 | 人数 | 占总人数比例 |
| 重视 | a | 0.3 |
| 一般 | 57 | 0.38 |
| 不重视 | b | c |
| 说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
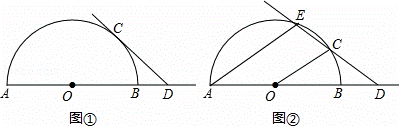
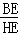 =
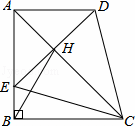
= ;③CD=2DH;④
;③CD=2DH;④ =
=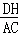 .
.

 ,
,  ,
,  ,
,  中,x可以取2和3的是()
中,x可以取2和3的是() 的解是 .
的解是 .