��Ŀ����
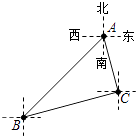
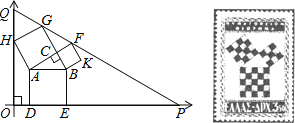
����Ŀ�����ɶ��������ƾõ���ʷ����������ܶ��˵���Ȥ��1955��ϣ�������˶�ö�Թ���ͼΪ��������Ʊ����ν����ͼ��ָ��ֱ�������ε�����Ϊ�������������ι��ɣ���������֤���ɶ���������ͼ�Ĺ���ͼ�У���֪��ACB=90�㣬��BAC=30�㣬AB=4������PQOʹ�á�O=90�㣬��Q����ֱ������ϵy���������ϣ���P��x���������ϣ���O��ԭ���غϣ���OQP=60�㣬��H�ڱ�QO�ϣ���D��E�ڱ�PO�ϣ���G��F�ڱ�PQ�ϣ���ô��P����Ϊ___________��
���𰸡���7![]() +6��0��
+6��0��
������������������ӳ�BA��QR�ڵ�M������AR��AP��

����ABC����GFC��

![]()
![]()
![]()
![]()
![]()
�֡�![]()
![]()
![]()
![]()
![]()
����QHG�ǵȱ�������.
![]()
��![]()
��![]() ��,
��, ![]()
��![]() ��
�У� ![]()
![]()
![]()
![]()
���P������Ϊ![]()
�ʴ�Ϊ�� ![]()

��ϰ��ϵ�д�
�����Ŀ