题目内容
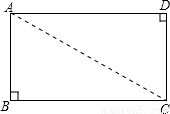
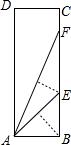 如图,矩形纸片ABCD沿过点B的直线折叠,点A落在BC边上的点E处,还原后,再沿过点E的直线折叠,点A落在BC边上的点F处,则tan∠FAB=( )
如图,矩形纸片ABCD沿过点B的直线折叠,点A落在BC边上的点E处,还原后,再沿过点E的直线折叠,点A落在BC边上的点F处,则tan∠FAB=( )分析:首先根据根据折叠可得:AB=BE,AE=EF,设AB=x,则EB=x,在Rt△AEB中利用勾股定理可得AE的长,进而得到EF的长,就可以得到FB的长,再根据三角函数的定义进而得到答案.
解答:解:根据折叠可得:AB=BE,AE=EF,
设AB=x,则EB=x,
在Rt△AEB中:AE=
=
x,
则EF=
x,BF=(
+1)x,
tan∠FAB=
=
+1,
故选:B.
设AB=x,则EB=x,
在Rt△AEB中:AE=
| AB2+EB2 |
| 2 |
则EF=
| 2 |
| 2 |
tan∠FAB=
| FB |
| AB |
| 2 |
故选:B.
点评:此题主要考查了图形的翻折变换,以及三角函数的定义,解决问题的关键是掌握翻折以后对应相等的线段AB=BE,AE=EF.

练习册系列答案
相关题目
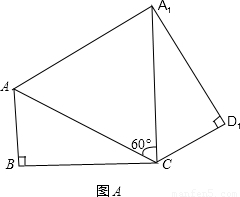
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4
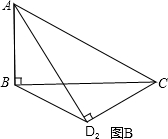

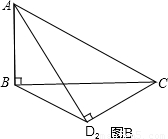
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
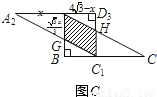
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



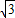 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: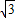 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.