题目内容
如图10-1-2(1),10-1-2(2),四边形ABCD是正方形,M是AB延长线上一点。直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F。【小题1】如图10-1-2(1),当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
③请证明你的上述两猜想。
【小题2】如图10-1-2(2),当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系。

【小题1】①DE=EF;②NE=BF③证明:∵四边形ABCD是正方形,N,E分别为AD,AB的中点,∴DN=EB∵BF平分∠CBM,AN=AE,∴∠DNE=∠EBF=90°+45°=135°∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF∴△DNE≌△EBF∴ DE=EF,NE=BF
【小题2】在DA边上截取DN=EB(或截取AN=AE),连结NE,点N就使得NE=BF成立(图略)
此时,DE=EF解析:
略

练习册系列答案
相关题目
某校为了对学生加强安全教育,对全校学生进行常规安全知识检测,老师从中随机抽取了部分学生的成绩(成绩为整数)按10分的组距分段,所得的统计结果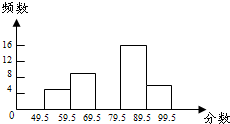 如图10所示的频数频数分布表和部分频数分布直方图.
如图10所示的频数频数分布表和部分频数分布直方图.
请结合图表完成下列问题:
(1)表中的a= ;b= ;c= .
(2)请把频数分布直方图补充完整;
(3)若此次检测中分数达到80分以上(含80分)为优秀,则所调查的学生的优秀率是 .
(4)若该校参加此次检测的学生共1800人,则分数达到60分以上(含60分)的学生约 人.
 如图10所示的频数频数分布表和部分频数分布直方图.
如图10所示的频数频数分布表和部分频数分布直方图.| 分 数 段 | 频 数 | 频 率 |
| 49.5~59.5 | 5 | 0.1 |
| 59.5~69.5 | a | 0.18 |
| 69.5~79.5 | 14 | 0.28 |
| 79.5~89.5 | 16 | b |
| 89.5~99.5 | 6 | 0.12 |
| c |
(1)表中的a=
(2)请把频数分布直方图补充完整;
(3)若此次检测中分数达到80分以上(含80分)为优秀,则所调查的学生的优秀率是
(4)若该校参加此次检测的学生共1800人,则分数达到60分以上(含60分)的学生约
 (2013•宝安区一模)已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.
(2013•宝安区一模)已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN. (2012•保定二模)△OAB在坐标系中的位置如图10所示
(2012•保定二模)△OAB在坐标系中的位置如图10所示 某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?,将收集到的数据整理,给出了如图10所示的统计图.
某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?,将收集到的数据整理,给出了如图10所示的统计图.