题目内容
（2002•昆明）已知：如图，AB=CD，CE∥DF，CE=DF．求证：AE=BF．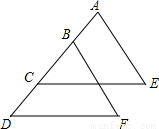
【答案】分析：欲证AE=BF，可证△ACE≌△BDF．
解答：证明：∵AB=CD，
∴AB+BC=CD+BC．
∴AC=BD．
又∵CE∥DF，
∴∠ACE=∠BDF．
在△ACE和△BDF中，
∵
，
∴△ACE≌△BDF（SAS）．
∴AE=BF．
点评：本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，在实际问题中，具体选用哪一个定理，根据已知条件而定．
解答：证明：∵AB=CD，
∴AB+BC=CD+BC．
∴AC=BD．
又∵CE∥DF，
∴∠ACE=∠BDF．
在△ACE和△BDF中，
∵
，∴△ACE≌△BDF（SAS）．
∴AE=BF．
点评：本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，在实际问题中，具体选用哪一个定理，根据已知条件而定．
练习册系列答案
春雨教育同步作文系列答案
相关题目
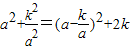（k为常数且k＞0，a≠0），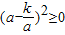
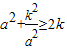
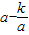=0，即
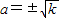时，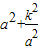
取得最小值2k．
？若存在，请求出m的值；若不存在，请说明理由．
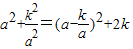（k为常数且k＞0，a≠0），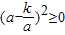
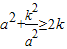
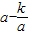=0，即
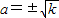时，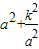
取得最小值2k．
？若存在，请求出m的值；若不存在，请说明理由．
