Question

如图1所示，一张半圆形纸片，直径AB=10，点C是半圆上的一个动点．沿半径CO把这张纸片剪出△AC₁O₁和△BC₂O₂两个三角形（如图2所示）．将纸片△AC₁O₁沿直线O₂B（AB）方向平移（点A，O₁，O₂，B始终在同一直线上），当点O₁与点B重合时，停止平移．在平移过程中，C₁O₁与BC₂交于点E，AC₁与C₂O₂，BC₂分别交于点F、P．
（1）当△AC₁O₁平移到如图3所示的位置时，猜想图中的O₁E与O₂F的数量关系，并证明你的猜想；
（2）若∠CAB=30°，设平移距离O₁O₂为x，△AC₁O₁与△BC₂O₂重叠部分面积为y，请写出y与x的函数关系式，以及自变量的取值范围；
（3）对于（2）中的结论是否存在这样的x的值，使重叠部分的面积等于原△ABC面积的

1

4

．若存在，求x的值；若不存在，请说明理由．

Answer 1

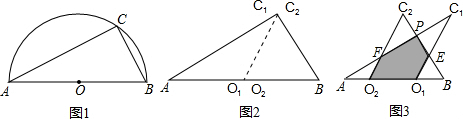
分析：（1）根据平移的性质，得O₁B=O₂A，再根据平行线等分线段定理即可证明；
（2）根据30°直角三角形的性质、相似三角形的性质进行求解；
（3）在（2）的基础上解一元二次方程即可．

解答：解：（1）O₁E=O₂F．理由如下：
∵O₁E∥O₂C₂，
∴

O1E

O2C2

=

O1B

O2B

，
同理

O2F

O1C1

=

O2A

O1A

，
根据平移的性质，知O₁B=O₂A，
∴O₁E=O₂F．

（2）∵AB是直径，
∴∠C=90°，
∴∠B=90°-30°=60°，
∴∠APB=90°．
在直角三角形APB中，AB=10-x，
则BP=

1

2

AB=5-

1

2

x，
则AP=5

3

-

3

2

x．
则直角三角形APB的面积是

3

8

x2-

5 3

2

x+

25

2

3

．
∵O₁E∥O₂C₂，
∴

S△O2C2B

S△O1EB

=

25

(5-x)2

，
则S_△O1EB=

1

4

3

(5-x)2，
则y=

3

8

x2-

5 3

2

x+

25

2

3

-2×

1

4

3

(5-x)2=-

3 3

8

x2+

5

2

3

x（0≤x≤5）．

（3）根据题意，得-

3 3

8

x2+

5

2

3

x=

1

4

×

25

2

3

，
解，得x=

5

3

或5．

点评：此题综合考查了相似三角形的判定及性质、圆周角定理、平移的性质以及三角形的面积公式，难度较大．
在求不规则图形的面积时，要哪个转化为规则图形的面积．