Question

如图，已知直线y=2x-6与双曲线y=

k

x

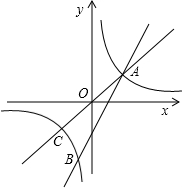（k＞0）交于A（x₁，y₁），B（x₂，y₂），并且x₁、x₂满足：x₁²+x₂²+x₁x₂=13．
（1）求双曲线y=

k

x

的表达式；
（2）设直线OA与双曲线的另一个交点为C，过原点O的另一条直线l交双曲线y=

k

x

于
M、N两点（点M在第一象限），若由点A、M、C、N为顶点组成的四边形的面积为24，求点M的坐标．

Answer 1

分析：（1）先利用韦达定理求出k的值，进一步写出表达式．
（2）通过图形面积分两种情况求出点M的坐标．

解答：解：（1）由

y=2x-6 y= k x

得：2x²-6x-k=0
∴

x1+x2=3  x1x2=- k 2

，
∵x₁²+x₂²+x₁x₂=13，∴（x₁+x₂）²-x₁x₂=13，即9+

k

2

=13，
解得：k=8，
所以双曲线y=

k

x

的表达式为：y=

8

x

．

（2）由（1）可得2x²-6x-8=0，
解得：x₁=4，x₂=-1，
∴A（4，2），B（-1，-8），
由对称性可知，
四边形AMCN为平行四边形，
∵四边形AMCN的面积=24，△OAM的面积=6，
设点M（m，

8

m

）（m＞0且m≠4），
①当0＜m＜4时，过A、M分别作x轴的垂线AD、ME，
则四边形ODAM的面积=△ODA的面积+△OAM的面积=△OEM的面积+梯形MEDA的面积，
∵△ODA的面积=△OEM的面积=4，∴梯形MEDA的面积=△OAM的面积=6，

1

2

（2+

8

m

）（4-m）=6，
m²+6m-16=0，∴m=2或m=-8（舍去），
②当m＞4时，同①可得：梯形MEDA的面积=6，

1

2

（2+

8

m

）（m-4）=6，
m²-6m-16=0，
m=8或m=-2（舍去），
综上所述：点M的坐标是（2，4）（8，1）．

点评：此题考查的知识点是反比例函数的综合应用，关键是运用韦达定理确定k的值，再通过图形面积分两种情况求出点M的坐标．