Question

【题目】已知线段AD＝80，点B、点C都是线段AD上的点．

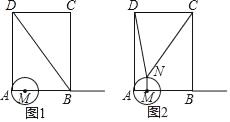
（1）如图1，若点M为AB的中点，点N为BD的中点，求线段MN的长；

（2）如图2，若BC＝10，点E是线段AC的中点，点F是线段BD的中点，求EF的长；

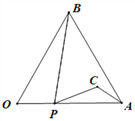
（3）如图3，若AB＝5，BC＝10，点P、Q分别从B、C出发向点D运动，运动速度分别为每秒移动1个单位和每秒移动4个单位，运动时间为t秒，点E为AQ的中点，点F为PD的中点，若PE＝QF，求t的值．

Answer 1

【答案】（1）MN＝40；（2）EF=35；（3）或t＝12．

【解析】

（1）由MN＝BM+BN＝即可求出答案；

（2）根据EF＝AD﹣AE﹣DF，可求出答案；

（3）可得PE＝AE﹣AB﹣BP＝，DF＝，则QF＝或，由PE＝QF可得方程，解方程即可得出答案．

解：（1）∵M为AB的中点，N为BD的中点，

∴，，

∴MN＝BM+BN＝＝；

（2）∵E为AC的中点，F为BD的中点，

∴，，

（3）运动t秒后，AQ＝AC+CQ＝15+4t，

∵E为AQ的中点，

∴，

∴，

∵DP＝DB﹣BP＝75﹣t，F为DP的中点，

∴，

又DQ＝DC﹣CQ＝65﹣4t，

∴，

或，

由PE＝QF得：=或=

解得：或t＝12．