题目内容
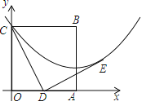
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),直线
的左侧),直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ..
..
(1)求抛物线与x轴的交点坐标;
(2)设点![]() 的横坐标为
的横坐标为![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
【答案】(1)![]() (-1,0),
(-1,0),![]() (5,0);(2)
(5,0);(2)![]() 或
或![]()
【解析】
(1)令y=0解方程即可解决问题.
(2)由题意P(m,m2+4m+5),E(m,![]() m+3),F(m,0),由PE=5EF,可得m2+4m+5(
m+3),F(m,0),由PE=5EF,可得m2+4m+5(![]() m+3)=5(
m+3)=5(![]() m+3),解方程即可解决问题.
m+3),解方程即可解决问题.
(1)对于抛物线![]()
令![]() ,则有
,则有![]()
解得:![]() ,
,![]()
又![]()
![]() 在
在![]() 的左侧
的左侧
![]()
![]() (-1,0),
(-1,0),![]() (5,0)
(5,0)
(2)![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]()
![]()
由题意,![]() ,即:
,即:![]()
①若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() .
.
由题意,![]() 的取值范围为:
的取值范围为:![]() ,故
,故![]() 、
、![]() 这两个解均舍去.
这两个解均舍去.
![]() 或
或![]()


练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目