Question

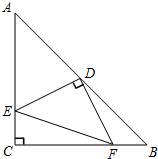已知Rt△ABC中，∠C=90°，AC=BC，D为AB边的中点，∠EDF=90°﹒现将∠EDF绕点D旋转，它的两边分别交AC、CB（或它们的延长线）于E、F（如图）．当∠EDF绕点D旋转到DE⊥AC于E时，S_△ABC、S_△DEF、S_△CEF的数量关系是

 

；当∠EDF绕点D旋转到DE和AC不垂直时，S_△ABC、S_△DEF、S_△CEF的数量关系是

 

．

Answer 1

分析：当∠EDF绕点D旋转到DE⊥AC于E时，连接CD，即可证得：△CDE≌△BDF，则S_△DEF+S_△CEF=S_△CDE+S_△CDF=S_△BDF+S_△CDF=

1

2

S_△ABC；
当∠EDF绕点D旋转到DE和AC不垂直时，连接CD，易得△CDE≌△BDF，则S_△CDE=S_△BDF，可以证得：S_△DEF=S_{多边形CEFBD}，则S_△DEF-S_△CEF=S_△BCD=

1

2

S_△ABC．

解答：（1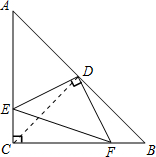）S_△DEF+S_△CEF=

1

2

S_△ABC 仍然成立．
证明：当∠EDF绕点D旋转到DE⊥AC于E时，连接CD．
∵Rt△ABC中，AC=BC，即△ABC为等腰直角三角形．
又∵D为AB边的中点，
∴CD=BD，∠ECD=∠FBD=45°，∠CDB=90°，
又∵∠EDF=90°，
∴∠EDF-∠CDF=∠CDB-∠CDF，即∠CDE=∠BDF，
在△CDE与△BDF中，
∵

∠ECD=∠FBD CD=BD ∠CDE=∠BDF

，
∴△CDE≌△BDF，
∴S_△CDE=S_△BDF，
∴S_△DEF+S_△CEF=S_△CDE+S_△CDF=S_△BDF+S_△CDF=S_△BCD=

1

2

S_△ABC，
得证．

（2）当∠EDF绕点D旋转到DE和AC不垂直时，
猜想 S_△DEF+S_△CEF=

1

2

S_△ABC，
证明：连接CD，
同理易得△CDE≌△BDF，
∴S_△CDE=S_△BDF，
∴S_△DEF+S_△CEF=S_{四边形DECF}=S_△CDE+S_△CDF=S_△DBF+S_△CDF=S_△BCD，
又∵S_△BCD=

1

2

S_△ABC，
则S_△DEF+S_△CEF=

1

2

S_△ABC．
故答案是：S_△DEF+S_△CEF=

1

2

S_△ABC，S_△DEF+S_△CEF=

1

2

S_△ABC．

点评：本题主要考查了旋转的性质，连接CD，证得△CDE≌△BDF是解决本题的关键．