题目内容
 如图,在⊙O中,AB、AC为互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,求⊙O的半径.
如图,在⊙O中,AB、AC为互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,求⊙O的半径.
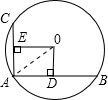 解:连接OA,
解:连接OA,∵AB⊥AC,OD⊥AB,OE⊥AC,
∴∠CAB=∠OEA=∠ODA=90°;
∴四边形OEAD是矩形;
∴OD=AE
∵点O为圆心,OD⊥AB,OE⊥AC,
∴AE=
 AC=6×
AC=6× =3cm,AD=
=3cm,AD= AB=8×
AB=8× =4cm;
=4cm;在Rt△OAD中,∠ODA=90°,OD=AE=3cm,AD=4cm
∴OA=
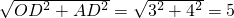 cm
cm即⊙O的半径为5cm.
分析:连接OA,易知四边形ODAE是矩形,则OE=AD,OD=AE;由垂径定理,可求得AE、AD的长,进而可在Rt△OAD(或Rt△OAE)中,由勾股定理求得半径的长.
点评:此题主要考查了垂径定理及勾股定理的综合应用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
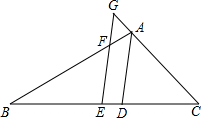 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.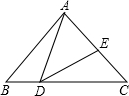 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.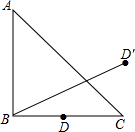 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=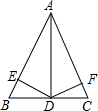 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有