题目内容
抛物线y=（x-1）（x-2）与坐标轴交点的个数为
- A.0
- B.1
- C.2
- D.3
D
分析：当x=0时，求出与y轴的纵坐标；当y=0时，求出与x轴的交点横坐标，从而求出与坐标轴的交点．
解答：当x=0时，y=2，
则与y轴的交点坐标为（0，2），
当y=0时，0=（x-1）（x-2），
解得x1=1，x2=2．
则与x轴的交点坐标为（1，0），（2，0）．
∴抛物线y=（x-1）（x-2）与坐标轴交点的个数为3个．
故选D．
点评：本题考查了抛物线与坐标轴的交点坐标，分别令x=0，y=0，将抛物线转化为方程是解题的关键．
分析：当x=0时，求出与y轴的纵坐标；当y=0时，求出与x轴的交点横坐标，从而求出与坐标轴的交点．
解答：当x=0时，y=2，
则与y轴的交点坐标为（0，2），
当y=0时，0=（x-1）（x-2），
解得x1=1，x2=2．
则与x轴的交点坐标为（1，0），（2，0）．
∴抛物线y=（x-1）（x-2）与坐标轴交点的个数为3个．
故选D．
点评：本题考查了抛物线与坐标轴的交点坐标，分别令x=0，y=0，将抛物线转化为方程是解题的关键．
练习册系列答案
相关题目
A和C，和x轴的另一个交点为B．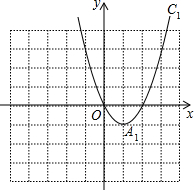
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．