题目内容
 当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD(矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:
当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD(矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在边AD上,折痕与BC交于点E;
(2)将纸片展平后,再一次折叠纸片,以点E所在直线为折痕,使点A落在BC上,折痕EF交AD于F,则∠AFE的度数为
考点:翻折变换(折叠问题),矩形的性质
专题:
分析:根据折叠的性质可得∠AEB=45°,再根据折叠的性质可得,即可求出∠FEC=(180°-45°)÷2,再根据平行线的性质即可求解.
解答: 解:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E点,∠AEB=45°,
解:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E点,∠AEB=45°,
(2)中,可得∠FEC=(180°-45°)÷2=67.5°,
∵AF∥EC,
∴∠AFE=∠FEC=67.5°.
故答案为:67.5°.
 解:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E点,∠AEB=45°,
解:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E点,∠AEB=45°,(2)中,可得∠FEC=(180°-45°)÷2=67.5°,
∵AF∥EC,
∴∠AFE=∠FEC=67.5°.
故答案为:67.5°.
点评:考查了折叠变换和学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
| 3 | 8 |
| A、2 | ||
| B、-2 | ||
| C、±2 | ||
D、±2
|
 如图,已知二次函数y=-x2+3x的对称轴与一次函数y=-2x的图象交于点A,则点A的坐标为
如图,已知二次函数y=-x2+3x的对称轴与一次函数y=-2x的图象交于点A,则点A的坐标为 正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积
正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积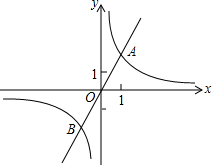 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=