题目内容
如图，直角三角形ABC中，∠ABC=90°，AB=6，以AB为直径画半圆，若阴影部分的面积S1-S2=
，则BC= ．
【答案】分析：分别表示出半圆内的空白面积，进而得出等式方程求出即可．
解答：
解：如图，连接BD，
∵直角三角形ABC中，∠ABC=90°，AB=6，以AB为直径画半圆，阴影部分的面积S1-S2=
，
∴S2-S1=-
，
∴
AB×BC-S2=
π×32-S1，
∴3BC=S2-S1+4.5π，
∴BC=
π．
故答案为：
π．
点评：此题主要考查了扇形的面积求法，利用△ABC减去S2等于半圆减去S1是解决问题的关键．
解答：
解：如图，连接BD，∵直角三角形ABC中，∠ABC=90°，AB=6，以AB为直径画半圆，阴影部分的面积S1-S2=
，∴S2-S1=-
，∴
AB×BC-S2=π×32-S1，∴3BC=S2-S1+4.5π，
∴BC=
π．故答案为：
π．点评：此题主要考查了扇形的面积求法，利用△ABC减去S2等于半圆减去S1是解决问题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
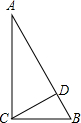如图，直角三角形ABC中∠ACB=90°，CD是高，∠A=30°，AB=4．则BD=
如图，直角三角形ABC的直角边AB=6，以AB为直径画半圆，若阴影部分的面积S1-S2=
如图在直角三角形ABC的斜边AB上另作直角三角形ABD，并以AB为斜边，若BC=1，AC=m，AD=2，则BD等于（ ）
如图，直角三角形ACB中，CD是斜边AB上的中线，若AC=8cm，BC=6cm，那么△ACD与△BCD的周长差为
如图，直角三角形ABC中，∠C=90°，P，E分别是边AB，BC上的点，D为△ABC外一点，DE⊥BC，DE=EC，BE=2EC，∠BDE=∠PEC，AD∥PE，AC=4，则线段BC的长为