题目内容
 如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,AE=2,则CD等于
如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,AE=2,则CD等于
- A.3
- B.4
- C.6
- D.8
D
分析:先根据AB为圆O的直径,弦CD⊥AB可知CD=2CE,再根据OC=5,AE=2可求出OE的长,利用勾股定理可求出CE的长,进而可求出答案.
解答:∵AB为圆O的直径,弦CD⊥AB,
∴CD=2CE,
∵OC=5,AE=2,
∴OA=5,
∴OE=OA-AE=5-2=3,
∴CE=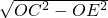 =
= =4.
=4.
∴CD=2CE=8
故选D.
点评:本题考查的是垂径定理及勾股定理,能根据垂径定理得出CD=2CE是解答此题的关键.
分析:先根据AB为圆O的直径,弦CD⊥AB可知CD=2CE,再根据OC=5,AE=2可求出OE的长,利用勾股定理可求出CE的长,进而可求出答案.
解答:∵AB为圆O的直径,弦CD⊥AB,
∴CD=2CE,
∵OC=5,AE=2,
∴OA=5,
∴OE=OA-AE=5-2=3,
∴CE=
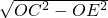 =
= =4.
=4.∴CD=2CE=8
故选D.
点评:本题考查的是垂径定理及勾股定理,能根据垂径定理得出CD=2CE是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
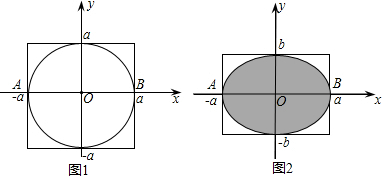 鸡蛋型”的椭球.已知半径为a的球的体积为
鸡蛋型”的椭球.已知半径为a的球的体积为 四边形是平行四边形.
四边形是平行四边形. x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).