Question

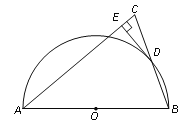
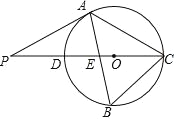
【题目】如图，已知⊙O的直径AB垂直弦CD于点E，连接AD、BC、OC，且OC＝5．

（1）若sin∠BCD=，求CD的长；

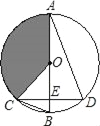
（2）若∠OCD＝4∠BCD，求扇形OAC（阴影部分）的面积（结果保留π）．

Answer 1

【答案】（1）CD＝9.6；（2）S＝．

【解析】

（1）由垂径定理可得CE=DE，在直角三角形OCE中，利用勾股定理可得CE的长，乘以2即为CD的长；

（2）算出∠COB的度数，也就求得了阴影部分的圆心角，利用扇形的面积公式计算即可．

（1）∵⊙O的直径AB垂直弦CD于点E，

∴CE＝DE

设EB＝3x，则BC＝5x，

∴CE＝4x，

在直角三角形OCE中，

OC2＝CE2+OE2，

52＝（4x）2+（5﹣3x）2，

解得x＝0或x＝1.2，

∴CE＝4x＝4.8，

∴CD＝2CE＝9.6；

（2）∵AB⊥CD，

∴

∴∠COB＝2∠BCD

∵∠OCD＝4∠BCD，∠OBC＝∠OCB，∠OCB+∠OBC+COB＝180°，

∴∠BCD＝15°，

∴∠OBC＝75°，

∴∠BOC＝30°，

∴∠AOC＝150°

∴S＝．