题目内容
已知:如图,N、M是以O为圆心,1为半径的圆上的两点,B是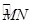 上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
小题1:四边形EPGQ (填“是”或者“不是”)平行四边形;
小题2:若四边形EPGQ是矩形,求OA的值;
小题3:连结PQ,求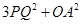 的值.
的值.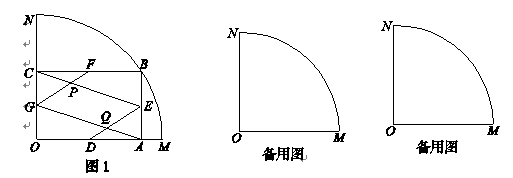
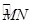 上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.小题1:四边形EPGQ (填“是”或者“不是”)平行四边形;
小题2:若四边形EPGQ是矩形,求OA的值;
小题3:连结PQ,求
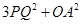 的值.
的值.
小题1:是
小题2:

小题3:
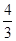
解:(1)是

(2)∵EPGQ是矩形.
∴∠CED=90°
∠AED+∠CEB =90°.
∵BA⊥OM,
∠BAO=90°
∴∠AED+∠EDA =90°
∴∠EDA=∠CEB.
∵BA⊥OM,BC⊥ON, ∠AOC =90°
∴OABC是矩形.
∴BC="OA," AB=OC
∠ABC=∠BAO=90°
∴△AED∽△BCE.∴ .
.
设OA=x,AB=y,
则
得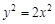 .又
.又 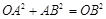 ,
,
即 .
.
∴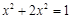 ,
,
解得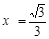 .
.
∴OA的值为
(2)连结GE交PQ于 ,过点P作OC的平行线分别交BC、GE于点
,过点P作OC的平行线分别交BC、GE于点 、
、 .
.

∵四边形PGQE是平行四边形
∴ .
.
∵BC∥GE
∴△PCF∽△PEG,
 ,
,
∴
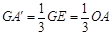 ,
,
∴ .
.
在Rt△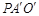 中,
中,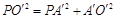 ,
,
即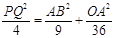 ,
,
又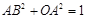 ,
,
∴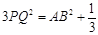 ,
,
∴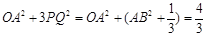 .说明:以上各题的其它解法只要正确.
.说明:以上各题的其它解法只要正确.

(2)∵EPGQ是矩形.
∴∠CED=90°
∠AED+∠CEB =90°.
∵BA⊥OM,
∠BAO=90°
∴∠AED+∠EDA =90°
∴∠EDA=∠CEB.
∵BA⊥OM,BC⊥ON, ∠AOC =90°
∴OABC是矩形.
∴BC="OA," AB=OC
∠ABC=∠BAO=90°
∴△AED∽△BCE.∴
 .
.设OA=x,AB=y,
则

得
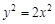 .又
.又 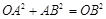 ,
,即
 .
.∴
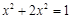 ,
,解得
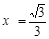 .
.∴OA的值为

(2)连结GE交PQ于
 ,过点P作OC的平行线分别交BC、GE于点
,过点P作OC的平行线分别交BC、GE于点 、
、 .
.
∵四边形PGQE是平行四边形
∴
 .
.∵BC∥GE
∴△PCF∽△PEG,
 ,
,∴

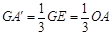 ,
,∴
 .
.在Rt△
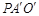 中,
中,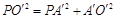 ,
,即
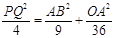 ,
,又
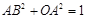 ,
,∴
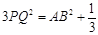 ,
, ∴
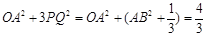 .说明:以上各题的其它解法只要正确.
.说明:以上各题的其它解法只要正确.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 b,得a2-b2=(
b,得a2-b2=(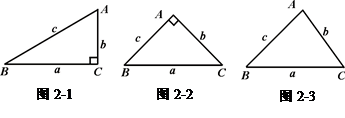

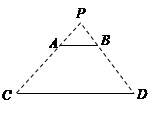


 ABC中,∠C=90°,两直角边AC、BC的长恰是方程
ABC中,∠C=90°,两直角边AC、BC的长恰是方程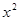 -4x+2=0的两个不同的根,则Rt
-4x+2=0的两个不同的根,则Rt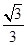 (B)
(B)
 (D)2
(D)2
 ,则
,则 = _______;已知线段a=9cm,c=4cm,线段b是a、c的比例中项,则b等于 cm.
= _______;已知线段a=9cm,c=4cm,线段b是a、c的比例中项,则b等于 cm.