题目内容
1. 如图,在△ABC中,∠ACB=90°,过点A做直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连接CE,已知BC=5,AC=12,则AE的长为11.9.
如图,在△ABC中,∠ACB=90°,过点A做直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连接CE,已知BC=5,AC=12,则AE的长为11.9.
分析 取CE的中点F,连接DF,由梯形中位线定理得出DF=$\frac{1}{2}$(BC+AE),设DF=x,则AE=2x-5,求出CE=2DF=2x,在Rt△ACE中,由勾股定理得出方程,解方程即可得出结果.
解答 解: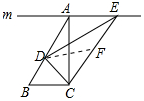 取CE的中点F,连接DF,
取CE的中点F,连接DF,
∵AE∥BC,D是AB的中点,
∴DF=$\frac{1}{2}$(BC+AE),
设DF=x,则AE=2x-5,
又DE⊥CD,F是CE的中点,
∴CE=2DF=2x,
在Rt△ACE中,由勾股定理得:122+(2x-5)2=(2x)2,
解得:x=8.45,
∴AE=2×8.45-5=11.9;
故答案为:11.9.
点评 本题考查了勾股定理、梯形中位线定理、平行线的性质等知识;由勾股定理得出方程是解决问题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
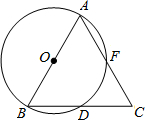 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.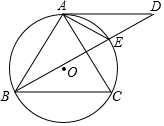 如图,⊙O为ABC的外接圆,AD为⊙O的切线,AD∥BC,BD交⊙O于E,且点E是$\widehat{AC}$的中点,连接AE.
如图,⊙O为ABC的外接圆,AD为⊙O的切线,AD∥BC,BD交⊙O于E,且点E是$\widehat{AC}$的中点,连接AE. 如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,EF交AD于点O,求证:OF=OE.
如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,EF交AD于点O,求证:OF=OE.