题目内容
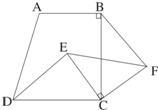 17、已知:梯形ABCD中,AB∥CD,∠ABC=90°,BC=CD,△ECF是等腰直角三角形,且连接BF、DE,请指出图中与BF相等的一条线段,并给予证明.
17、已知:梯形ABCD中,AB∥CD,∠ABC=90°,BC=CD,△ECF是等腰直角三角形,且连接BF、DE,请指出图中与BF相等的一条线段,并给予证明.分析:由AB∥CD,∠ABC=90°,∠ECF=90°得∠ECD=∠FCB,又因为BC=CD,EC=CF,则利用SAS判定△DCE≌△BCF,根据全等三角形的对应边相等可得到DE=BF.
解答:解:DE=BF.
证明:∵AB∥CD,∠ABC=90°,
∴∠BCD=90°.
∵∠ECF=90°,
∴∠ECD=∠FCB.
∵BC=CD,EC=CF,
∴△DCE≌△BCF.
∴DE=BF.
证明:∵AB∥CD,∠ABC=90°,
∴∠BCD=90°.
∵∠ECF=90°,
∴∠ECD=∠FCB.
∵BC=CD,EC=CF,
∴△DCE≌△BCF.
∴DE=BF.
点评:此题主要考查学生对梯形的性质及全等三角形的判定方法的理解及运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
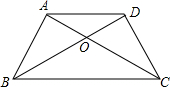 如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.
如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.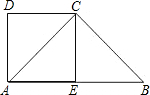 已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=
已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC= 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )
11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( ) 如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )
如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )