Question

【题目】二次函数y＝ax2+bx+2的图象交x轴于点A（﹣1，0），点B（4，0）两点，交y轴于点C．动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．

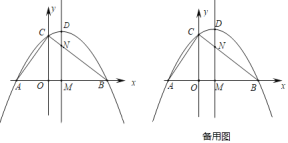
（1）求二次函数y＝ax2+bx+2的表达式；

（2）连接BD，当t＝时，求△DNB的面积；

（3）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标．

Answer 1

【答案】（1）；（2）2；（3）D（1，3）或D（3，2）．

【解析】

（1）根据二次函数经过A，B两点，分别代入二次函数解析式，解二元一次方程组即可求出a和b的值.

（2）根据B，C两点可以求出直线BC的解析式，再根据t＝可以求出N点和D点坐标，然后求出△DBM的面积与△BMN的面积，根据 可求求△DNB的面积.

（3）PC2＝（2t﹣1）2+（m﹣2）2，PB2＝（2t﹣5）2+m2，PB＝PC，则（2t﹣1）2+（m﹣2）2＝（2t﹣5）2+m2，且PC⊥PB，＝＝﹣1，即可求解．

（1）将点A（﹣1，0），B（4，0）代入y＝ax2+bx+2，

∴a＝﹣，b＝，

∴y＝﹣x2+x+2；

（2）C（0，2），

∴BC的直线解析式为y＝﹣x+2，

当t＝时，AM＝3，

∵AB＝5，

∴MB＝2，

∴M（2，0），N（2，1），D（2，3），

∴△DNB的面积＝△DMB的面积﹣△MNB的面积＝MB×DM﹣MB×MN＝×2×2＝2.

（3）∵BM＝5﹣2t，

∴M（2t﹣1，0），

设P（2t﹣1，m），

∵PC2＝（2t﹣1）2+（m﹣2）2，PB2＝（2t﹣5）2+m2，

∵PB＝PC，

∴（2t﹣1）2+（m﹣2）2＝（2t﹣5）2+m2，

∴m＝4t﹣5，

∴P（2t﹣1，4t﹣5），

∵PC⊥PB，

∴＝＝﹣1

∴t＝1或t＝2，

∴M（1，0）或M（3，0），

∴D（1，3）或D（3，2）．