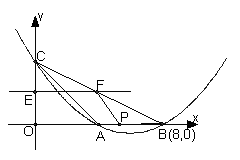
题目内容
如图,抛物线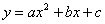 关于直线
关于直线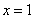 对称,与坐标轴交于
对称,与坐标轴交于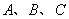 三点,且
三点,且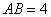 ,点
,点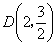 在抛物线上,直线是一次函数
在抛物线上,直线是一次函数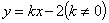 的图象,点
的图象,点 是坐标原点.
是坐标原点.
(1)求抛物线的解析式;
(2)若直线平分四边形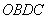 的面积,求
的面积,求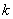 的值.
的值.
(3)把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线交于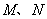 两点,问在
两点,问在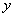 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点 ,使得不论
,使得不论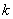 取何值,直线
取何值,直线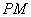 与
与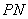 总是关于
总是关于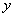 轴对称?若存在,求出
轴对称?若存在,求出 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
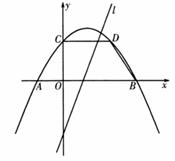
(1)因为抛物线关于直线x=1对称,AB=4,所以A(-1,0),B(3,0),
由点D(2,1.5)在抛物线上,所以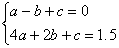 ,所以3a+3b=1.5,即a+b=0.5,
,所以3a+3b=1.5,即a+b=0.5,
又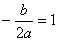 ,即b=-2a,代入上式解得a=-0.5,b=1,从而c=1.5,所以
,即b=-2a,代入上式解得a=-0.5,b=1,从而c=1.5,所以 .
.
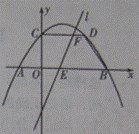
(2)由(1)知 ,令x=0,得c(0,1.5),所以CD//AB,
,令x=0,得c(0,1.5),所以CD//AB,
令kx-2=1.5,得l与CD的交点F(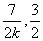 ),
),
令kx-2=0,得l与x轴的交点E(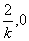 ),
),
根据S四边形OEFC=S四边形EBDF得:OE+CF=DF+BE,
即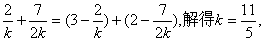
(3)由(1)知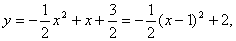
所以把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为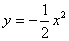
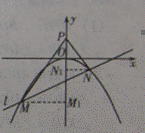
假设在y轴上存在一点P(0,t),t>0,使直线PM与PN关于y轴对称,过点M、N分别向y轴作垂线MM1、NN1,垂足分别为M1、N1,因为∠MPO=∠NPO,所以Rt△MPM1∽Rt△NPN1,
所以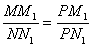 ,………………(1)
,………………(1)
不妨设M(xM,yM)在点N(xN,yN)的左侧,因为P点在y轴正半轴上,
则(1)式变为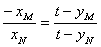 ,又yM =k xM-2, yN=k xN-2,
,又yM =k xM-2, yN=k xN-2,
所以(t+2)(xM +xN)=2k xM xN,……(2)
把y=kx-2(k≠0)代入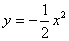 中,整理得x2+2kx-4=0,
中,整理得x2+2kx-4=0,
所以xM +xN=-2k, xM xN=-4,代入(2)得t=2,符合条件,
故在y轴上存在一点P(0,2),使直线PM与PN总是关于y轴对称.

若 ,则
,则 的值为( )
的值为( )
| A. |
| B. |
| C. |
| D. |
|
 ( )
( )







 的所有正整数解________________.
的所有正整数解________________.




 ,
, ,
, ,-1的平均数为1,则这组数据的极差是____________.
,-1的平均数为1,则这组数据的极差是____________. 的值为 ( )
的值为 ( ) 


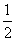 ,△ABC的面积为8.
,△ABC的面积为8.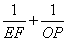 的值最小,并求出最小值.
的值最小,并求出最小值.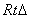 ;若存在,请直接写出t的值.
;若存在,请直接写出t的值.