Question

已知：如图，在△ABC中，∠1=∠2，DE∥AC，求证：．

Answer 1

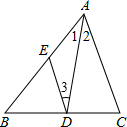证明：如右图所示，
∵DE∥AC，
∴∠2=∠3，
∵∠1=∠2，
∴∠1=∠3，
∴AE=DE，
∵DE∥AC，
∴△BED∽△BAC，
∴=，
∴=，
∵+===，
==，
∴+=，
∴+=．
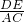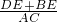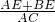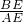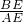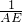分析：根据DE∥AC，易知∠2=∠3，而∠1=∠2，那么∠1=∠3，根据等角对等边看可知AE=DE，根据DE∥AC，结合平行线分线段成比例定理的推论可得△BED∽△BAC，那么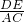=，变形得=，在所证的等式两边同乘以BE，分别转化计算，易证两个式子相等，从而得证．
点评：本题考查了相似三角形的判定和性质、平行线分线段成比例定理的推论，解题的关键是证明AE=DE，以及△BED∽△BAC，此题采用的是两端向中间的证明方法．