Question

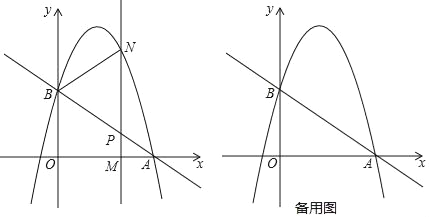
【题目】如图，Rt△ABC中，∠C=90°，∠A=30°，BC=2，CD是斜边AB上的高，点E为边AC上一点（点E不与点A、C重合），联结DE，作CF⊥DE，CF与边AB、线段DE分别交于点F、G；

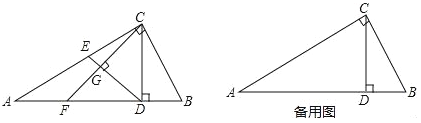
（1）求线段CD、AD的长；

（2）设CE=x，DF=y，求y关于x的函数解析式，并写出它的定义域；

（3）联结EF，当△EFG与△CDG相似时，求线段CE的长．

Answer 1

【答案】（1）CD=，AD=；

（2）y=﹣1，（≤x＜2）；

（3）CE=或；

【解析】

试题分析：（1）利用特殊角的三角函数可知sin∠B=，tan∠A=，由此求得线段CD、AD的长；

（2）证得△CDE∽△BFC，得出，整理得出答案即可；

（3）分两种情况考虑：①当△EGF∽△DGC时；②当△FEG∽△CGD时；利用相似的性质探讨得出答案即可．

试题解析：（1）在Rt△BCD中，

BC=2，∠B=90°﹣∠A=60°，

sin∠B=，

即CD=×2=，

同理tan∠A=，

AD=3；

（2）∵∠CDE=∠BFC=90°﹣∠DCF，∠ECD=∠B=60°，

∴△CDE∽△BFC，

∴，

即，

∴y=﹣1，（≤x＜2）；

（3）∠EGF=∠CGD=90°

①当△EGF∽△DGC时，∠GEF=∠GDC，

∴EF∥DC，

∴，

解得x=；

②当△FEG∽△CGD时，

∴∠GEF=∠GCD=∠GDF，

∴EF=DF，

又∵CF⊥DE，

∴EG=DG，

∴CD=CE=；

综上，CE=或；