题目内容
(1)如图1,AB⊥BD于B,DE⊥BD于D,已知AB=CD,BC=ED.求∠ACE的度数.
(2)如图2,△ABE与△CDA中,∠C=∠CAE=90°,AB=CD,AE=AC.问这两个直角三角形的边AD与EB之间有何关系?并说明理由(几何图形的线段关系包括大小与位置关系)

(2)如图2,△ABE与△CDA中,∠C=∠CAE=90°,AB=CD,AE=AC.问这两个直角三角形的边AD与EB之间有何关系?并说明理由(几何图形的线段关系包括大小与位置关系)

分析:(1)根据SAS推出△ABC≌△CDE,推出∠E=∠ACB,求出∠ACE=90°即可;
(2)根据SAS推出△ABC≌△CDE,推出∠E=∠ACB,AD=BE,求出∠ACE=90°即可.
(2)根据SAS推出△ABC≌△CDE,推出∠E=∠ACB,AD=BE,求出∠ACE=90°即可.
解答:(1)解:∵AB⊥BD,DE⊥BD,
∴∠B=∠CDE=90°,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(SAS),
∴∠E=∠ACB,
∵∠ECD+∠E=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°.
(2)解:AD=EB且AD⊥EB
理由:∵在△ABC和△CDE中,
,
∴△ABC≌△CDE(SAS),
∴AD=BE,∠BEA=∠DAC,
∵∠EAD+∠DAC=90°,
∴∠BEA+∠EAD=90°,
∴AD⊥EB,
即AD=EB 且 AD⊥EB.
∴∠B=∠CDE=90°,
在△ABC和△CDE中,
|
∴△ABC≌△CDE(SAS),
∴∠E=∠ACB,
∵∠ECD+∠E=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°.
(2)解:AD=EB且AD⊥EB
理由:∵在△ABC和△CDE中,
|
∴△ABC≌△CDE(SAS),
∴AD=BE,∠BEA=∠DAC,
∵∠EAD+∠DAC=90°,
∴∠BEA+∠EAD=90°,
∴AD⊥EB,
即AD=EB 且 AD⊥EB.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的性质是:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 如图,如果AB∥CD,那么下面说法错误的是( )
如图,如果AB∥CD,那么下面说法错误的是( ) 如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.
如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF. 如图,直线AB、CD被直线CE所截.
如图,直线AB、CD被直线CE所截.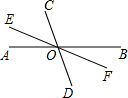 如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( )
如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( ) 如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.
如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.