题目内容
 已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为
已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为
- A.45°
- B.35°
- C.25°
- D.20°
A
分析:直接根据圆周角定理进行解答即可.
解答:∵OA⊥OB,
∴∠AOB=90°,
∴∠ACB= ∠AOB=45°.
∠AOB=45°.
故选A.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
分析:直接根据圆周角定理进行解答即可.
解答:∵OA⊥OB,
∴∠AOB=90°,
∴∠ACB=
 ∠AOB=45°.
∠AOB=45°.故选A.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 25、已知,如图,OA⊥OB,OD平分∠AOC,∠BOC=40°.求∠AOD的度数.
25、已知,如图,OA⊥OB,OD平分∠AOC,∠BOC=40°.求∠AOD的度数.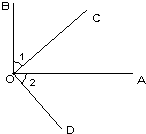
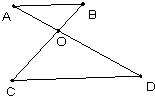
 13、已知:如图,OA,OB为⊙O的半径,C,D分别为OA,OB的中点,求证:AD=BC.
13、已知:如图,OA,OB为⊙O的半径,C,D分别为OA,OB的中点,求证:AD=BC. 40、已知:如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点.求证:MC=NC.
40、已知:如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点.求证:MC=NC. (2013•鞍山)已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
(2013•鞍山)已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )