题目内容
将长为24的线段截成长度为整数的三段,使它们成为一个三角形的三边,则构成的三角形是等腰三角形的概率是
- A.

- B.
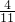
- C.

- D.

A
分析:将长为24的线段截成长度为整数的三段,将能组成三角形的线段列举出来,利用概率公式解答即可.
解答:当三边分别为6,6,12时,恰不能构成三角形;
故三边为
6,7,11;
6,8,10;
6,9,9;
7,7,10;
7,8,9;
8,8,8;
8,11,5;
9,10,5;
9,11,4;
10,10,4;
10,11,3;
11,11,2;
共12种情况,
等腰三角形有6,9,9;7,7,10;8,8,8;10,10,4;11,11,2;
则构成的三角形是等腰三角形的概率是 .
.
故选A.
点评:此题主要考查了概率公式,同时考查了例举法及三角形的三边关系,有一定的难度,注意列举时要做到不重不漏.
分析:将长为24的线段截成长度为整数的三段,将能组成三角形的线段列举出来,利用概率公式解答即可.
解答:当三边分别为6,6,12时,恰不能构成三角形;
故三边为
6,7,11;
6,8,10;
6,9,9;
7,7,10;
7,8,9;
8,8,8;
8,11,5;
9,10,5;
9,11,4;
10,10,4;
10,11,3;
11,11,2;
共12种情况,
等腰三角形有6,9,9;7,7,10;8,8,8;10,10,4;11,11,2;
则构成的三角形是等腰三角形的概率是
 .
.故选A.
点评:此题主要考查了概率公式,同时考查了例举法及三角形的三边关系,有一定的难度,注意列举时要做到不重不漏.

练习册系列答案
相关题目
将长为24的线段截成长度为整数的三段,使它们成为一个三角形的三边,则构成的三角形是等腰三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|



