题目内容
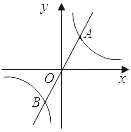
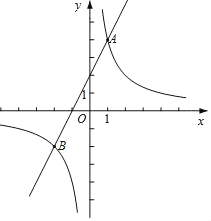
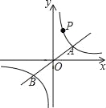
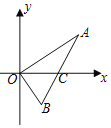
【题目】如图，在直角坐标平面xOy中，点A坐标为
，
，
，AB与x轴交于点C，那么AC：BC的值为______．
【答案】
【解析】
过点A作AD⊥y轴，垂足为D，作BE⊥y轴，垂足为E.先证△ADO∽△OEB，再根据∠OAB＝30°求出三角形的相似比，得到OD:OE=2∶
，根据平行线分线段成比例得到AC:BC=OD:OE=2∶=
解：
如图所示：过点A作AD⊥y轴，垂足为D，作BE⊥y轴，垂足为E.
∵∠OAB＝30°，∠ADE＝90°，∠DEB＝90°
∴∠DOA+∠BOE＝90°，∠OBE+∠BOE＝90°
∴∠DOA=∠OBE
∴△ADO∽△OEB
∵∠OAB＝30°，∠AOB＝90°，
∴OA∶OB=
∵点A坐标为（3，2）
∴AD=3，OD=2
∵△ADO∽△OEB
∴
∴OE
∵OC∥AD∥BE
根据平行线分线段成比例得：
AC:BC=OD:OE=2∶=
故答案为.
练习册系列答案
相关题目
