Question

正三角形的外接圆的半径和高的比为（　　）

• A．1：2
• B．2：3
• C．3：4
• D．1：

  3

Answer 1

分析：连接OB，AO，延长AO交BC于D，根据⊙O是等边三角形ABC的外接圆求出∠OBC=30°，推出OB=2OD，求出AD=

3

2

OB，代入求出即可．

解答：解：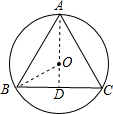
连接OB，AO，延长AO交BC于D，
∵⊙O是等边三角形ABC的外接圆，
∴AD⊥BC，∠OBC=

1

2

∠ABC=

1

2

×60°=30°，
∵∠ADB=90°，∠OBC=30°，
∴OD=

1

2

OB，
∵AD=OA+OD，
∴AD=OB+

1

2

OB=

3

2

OB，
即OB：AD=OB：（

3

2

OB）=2：3．
故选B．

点评：本题考查了等边三角形性质，三角形的外接圆与外心，含30度角的直角三角形等知识点的应用，关键是求出OD=

1

2

OB，主要考查学生的理解能力和推理能力．