Question

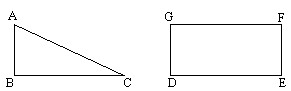
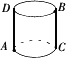
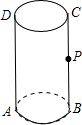如图，P为圆柱ABCD的母线BC的中点，已知圆柱母线长为4，底面半径OA=1．则在圆柱的侧面上点P到点A的最短距离为（　　）

• A、2

  2

• B、

  4+π2

• C、2π2
• D、

  2+π2

Answer 1

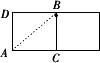
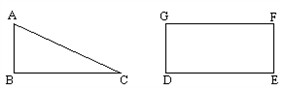
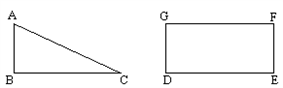
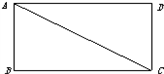
分析：要求圆柱的侧面上点P到点A的最短距离，将圆柱的侧面展开，得到一个矩形，然后利用两点之间线段最短解答．

解答：解：由题意知，展开后得到的矩形长为2π÷2=π，宽为4÷2=2，
根据勾股定理求得AP=

4+π2

．
故在圆柱的侧面上点P到点A的最短距离为

4+π2

．
故选B．

点评：本题考查了平面展开-最短路径问题．圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，宽等于圆柱的母线长．本题就是把圆柱的侧面展开成矩形，“化曲面为平面”，用勾股定理解决．注意要求的线段所在的直角三角形的两直角边分别为圆柱底面周长的一半，圆柱的母线长的一半．