题目内容
已知2x=y,m是任意有理数,下列等式不一定成立的是
- A.2x-m=y-m
- B.2mx=my
- C.2(m-1)•3x=(m-1)•3y
- D.
 =
=
D
分析:由2x=y,m是任意有理数,根据等式的基本性质分析求解即可求得答案,注意除以一个不为零的数,结果仍得等式.注意排除法在解选择题中的应用.
解答:∵2x=y,m是任意有理数,
∴2x-m=y-m,2mx=my,
故A,B成立;
∴2x=y,3(m-1)是任意有理数,
∴2(m-1)•3x=(m-1)•3y正确,
故C成立;
∵m是任意有理数,
∴m-3有可能等于0,
∴ =
= 当m=3是不成立.
当m=3是不成立.
故D不一定成立.
故选D.
点评:此题考查了等式的基本性质.注意性质1、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
分析:由2x=y,m是任意有理数,根据等式的基本性质分析求解即可求得答案,注意除以一个不为零的数,结果仍得等式.注意排除法在解选择题中的应用.
解答:∵2x=y,m是任意有理数,
∴2x-m=y-m,2mx=my,
故A,B成立;
∴2x=y,3(m-1)是任意有理数,
∴2(m-1)•3x=(m-1)•3y正确,
故C成立;
∵m是任意有理数,
∴m-3有可能等于0,
∴
 =
= 当m=3是不成立.
当m=3是不成立.故D不一定成立.
故选D.
点评:此题考查了等式的基本性质.注意性质1、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.

练习册系列答案
相关题目
 (2012•义乌市)如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
(2012•义乌市)如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: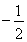
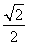
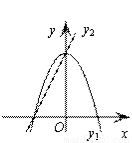
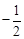 或
或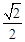 .
.