题目内容
如图,已知⊙O中,弦BC=8,A是BAC的中点,弦AD与BC交于点E,
AE=5![]() ,ED=
,ED=![]() ,M为弧BDC上的动点,(不与B、C重合),AM交BC于N.
,M为弧BDC上的动点,(不与B、C重合),AM交BC于N.
(1)求证:AB2=AE·AD;
(2)当M在弧BDC上运动时,问AN·AM、AN·NM中有没有值保持不变的?有的话,试求出此定值;若不是定值,请求出其最大值;
(3)若F是CB延长线上一点,FA交⊙O于G,当AG=8时,求sin∠AFB的值.

如图(1),证明:(1)连BD
∵![]() ∴∠ABC=∠ADB
∴∠ABC=∠ADB
又∵∠BAE=∠DAB ∴△ABE∽△ADB
∴![]() ∴
∴![]()
(2)连结BM,图(2)同(1)可证△ABM∽△ANB,
则![]() ∴
∴![]()
∴![]() =
=![]()
即![]() 为定值. 设BN=x,则CN=(8-x)
为定值. 设BN=x,则CN=(8-x)
∵![]()
![]()
故当BN=x=4时, ![]() 有最大值为16.
有最大值为16.
(3)作直径AH交BC于K,连结GH,如图(3),
∵A是弧BAC的中点 ∴AH⊥BC,且![]()
∴![]()
∴AK=8又由![]() 得:
得: ![]()
∴AH=10 又∵∠AGH=∠BKF=90°,
且∠GAH=∠KAF,∴∠F=∠H
 ∴sin
∴sin![]() sin
sin![]()

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
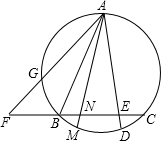 如图,已知⊙O中,弦BC=8,A是
如图,已知⊙O中,弦BC=8,A是
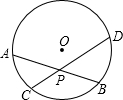 如图,已知⊙O中,弦AB与CD相交于点P.
如图,已知⊙O中,弦AB与CD相交于点P.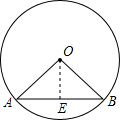 如图,已知⊙O中,弦AB=12cm,O点到AB的距离等于AB的一半,则∠AOB的度数为
如图,已知⊙O中,弦AB=12cm,O点到AB的距离等于AB的一半,则∠AOB的度数为 如图,已知⊙O中,弦AC、BD相交于点P,AB=5,AP=3,DP=2,则CD=
如图,已知⊙O中,弦AC、BD相交于点P,AB=5,AP=3,DP=2,则CD=