题目内容
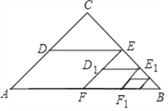
【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1；取BE中点E1，作E1D1∥FB，E1F1∥EF,得到四边形E1D1FF1，它的面积记作S2，照此规律作下去,则S1=_______，S2017=____________．
【答案】 1 
．
【解析】∵∠C=90，AC=BC=2，
∴△ABC的面积为： 
×2×2=2，
∵点E为BC边中点,ED∥AB，
∴△CDE∽△CAB，
∴
，
∴S△CDE=
，
同∵EF∥AC，点E为BC边中点，
∴S△BEF=
，
∴S=1，
同理,S=
,S=
，
以此类推, 
.
故答案为：1; 
.
点睛;本题考查了三角形中位线定理，等边三角形的性质，三角形的中位线平行于第三边，并且等于第三边的一半.
练习册系列答案
相关题目
