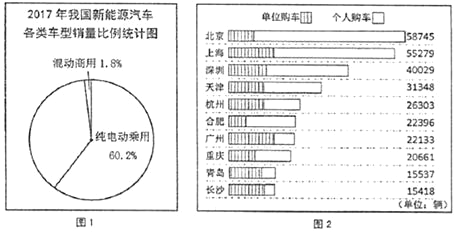
ЬтФПФкШн
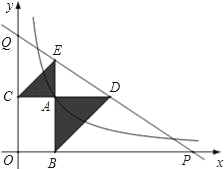
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+c(aЁй0)ОЙ§AЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉШ§ЕуЃЌЦфЖЅЕуЮЊDЃЌСЌНгBDЃЌЕуЪЧЯпЖЮBDЩЯвЛИіЖЏЕуЃЈВЛгыBЁЂDжиКЯЃЉЃЌЙ§ЕуPзїyжсЕФДЙЯпЃЌДЙзуЮЊEЃЌСЌНгBEЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЌВЂаДГіЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉШчЙћPЕуЕФзјБъЮЊЃЈxЃЌyЃЉЃЌЁїPBEЕФУцЛ§ЮЊЃЌЧѓSгыxЕФКЏЪ§ЙиЯЕЪНЃЌаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЌВЂЧѓГіSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБSШЁЕУзюДѓжЕЪБЃЌЙ§ЕуPзїxЕФДЙЯпЃЌДЙзуЮЊFЃЌСЌНгEFЃЌАбЁїPEFбижБЯпEFелЕўЃЌЕуPЕФЖдгІЕуЮЊPЁфЃЌЧыжБНгаДГіPЁфЕузјБъЃЌВЂХаЖЯЕуPЁфЪЧЗёдкИУХзЮяЯпЩЯЃЎ

ЁОД№АИЁПЃЈ1ЃЉЖЅЕуDЕФзјБъЮЊ(1ЃЌ4)ЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌ SШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌ SШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉАбPЁфзјБъЃЈ
ЃЛЃЈ3ЃЉАбPЁфзјБъЃЈ![]() ЃЉДњШыХзЮяЯпНтЮіЪНЃЌВЛГЩСЂЃЌЫљвд
ЃЉДњШыХзЮяЯпНтЮіЪНЃЌВЛГЩСЂЃЌЫљвд![]() ВЛдкХзЮяЯпЩЯЃЎ
ВЛдкХзЮяЯпЩЯЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнAЃЌBЃЌCШ§ЕуЕФзјБъЃЌПЩвддЫгУНЛЕуЪНЗЈЧѓЕУХзЮяЯпЕФНтЮіЪНЃЎдйИљОнЖЅЕуЕФзјБъЙЋЪНЧѓЕУХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈ2ЃЉИљОнBЃЌDЕФзјБъдЫгУД§ЖЈЯЕЪ§ЗЈЧѓЕУжБЯпBDЕФНтЮіЪНЃЌдйИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНвдМАyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЕУЕНsгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎЕуPЕФКсзјБъМДxЕФжЕЮЛгкЕуDКЭЕуBЕФКсзјБъжЎМфЃЎИљОнЖўДЮКЏЪ§ЕФЖЅЕуЪНМДПЩЗжЮіЦфзюжЕЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉжаЕФзјБъЕУЕуEКЭЕуCжиКЯЃЎЙ§PЁфзїPЁфHЁЭyжсгкHЃЌPЁфFНЛyжсгкЕуMЃЎвЊЧѓPЁфHКЭOHЕФГЄЃЎPЁфHЕФГЄПЩвддЫгУжБНЧШ§НЧаЮPЁфCMЕФУцЛ§НјааМЦЫуЃЎЩшMCЃНmЃЌдђMFЃНmЃЌPЁфMЃН3mЃЌPЁфEЃН32ЃЎИљОнЙДЙЩЖЈРэСаЗНГЬЧѓНтЃЌЕУЕНжБНЧШ§НЧаЮPЁфCMЕФШ§БпКѓЃЌдйИљОнжБНЧШ§НЧаЮЕФУцЛ§ЙЋЪННјааМЦЫуЃЎвЊЧѓOHЕФГЄЃЌвбжЊЕуCЕФзјБъЃЌжЛашИљОнЙДЙЩЖЈРэНјвЛВНЧѓЕУCHЕФГЄМДПЩЃЎАбЧѓЕУЕФЕуPЕФзјБъДњШыХзЮяЯпНтЮіЪНМДПЩХаЖЯЕуPЁфЪЧЗёдкИУХзЮяЯпЩЯЃЎ
ЃЈ1ЃЉЩш![]() ЃЌ
ЃЌ
Аб![]() ДњШыЃЌЕУ
ДњШыЃЌЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшжБЯп![]() НтЮіЪНЮЊЃК
НтЮіЪНЮЊЃК![]() ЃЈ
ЃЈ![]() ЃЉЃЌАб
ЃЉЃЌАб![]() СНЕузјБъДњШыЃЌ
СНЕузјБъДњШыЃЌ
ЕУ![]()
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯп![]() НтЮіЪНЮЊ
НтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ
ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБ![]() ШЁЕУзюДѓжЕЃЌ
ШЁЕУзюДѓжЕЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ
зїЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ
ЗЈвЛЃКЙ§![]() зї
зї![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌ
ЃЌ
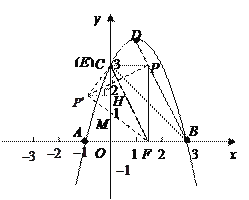
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
дк![]() жаЃЌгЩЙДЙЩЖЈРэЃЌ
жаЃЌгЩЙДЙЩЖЈРэЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() зјБъ
зјБъ![]() ЃЛ
ЃЛ
ЗЈЖўЃКСЌНг![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌЗжБ№Й§Еу
ЃЌЗжБ№Й§Еу![]() зї
зї![]() ЕФДЙЯпЃЌДЙзуЮЊ
ЕФДЙЯпЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ
взжЄ![]() ЃЌ
ЃЌ
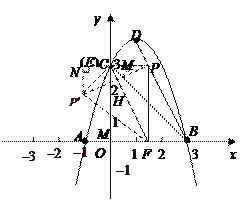
Ёр![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩШ§НЧаЮжаЮЛЯпЖЈРэЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() зјБъ
зјБъ![]() ЃЎ
ЃЎ
Аб![]() зјБъ
зјБъ![]() ДњШыХзЮяЯпНтЮіЪНЃЌВЛГЩСЂЃЌЫљвд
ДњШыХзЮяЯпНтЮіЪНЃЌВЛГЩСЂЃЌЫљвд![]() ВЛдкХзЮяЯпЩЯЃЎ
ВЛдкХзЮяЯпЩЯЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ