题目内容
13、已知MN是⊙O的切线，AB是⊙O的直径．求证：点A、B与MN的距离的和为定值．
分析：此题需要根据题意画出图形，利用切线的性质，得出所作三条线是垂直关系，再利用平行线分线段成比例定理可以证明．
解答：
证明：根据题意可画出图形，过点A做AC⊥MN于点C，过点B做BD⊥MN于点D，连接OE
∵MN是⊙O的切线
∴OE⊥MN
∴AC∥OE∥BD
又∵O为AB中点，
∴OE为梯形ACDB的中位线，
∴AC+BD=2OE
即AC+BD等于定长，为圆的直径．
以上可得：点A、B与MN的距离的和为定值
证明：根据题意可画出图形，过点A做AC⊥MN于点C，过点B做BD⊥MN于点D，连接OE∵MN是⊙O的切线
∴OE⊥MN
∴AC∥OE∥BD
又∵O为AB中点，
∴OE为梯形ACDB的中位线，
∴AC+BD=2OE
即AC+BD等于定长，为圆的直径．
以上可得：点A、B与MN的距离的和为定值
点评：此题主要考查了平行线分线段成比例定理，以及梯形中位线的性质，题目非常典型．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
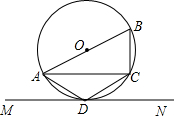如图所示，AB是⊙O的直径，D是圆上一点，
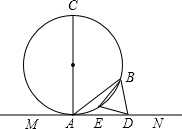已知：如图，AC是⊙O的直径，AB是弦，MN是过点A的直线，AB等于半径长．
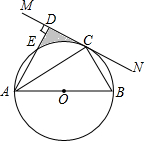（2012•乌鲁木齐）如图，AB是⊙O的直径，C为圆周上的一点，过点C的直线MN满足∠MCA=∠CBA．