题目内容
 如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约
如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约| 5 | 3 |
分析:知道抛物线顶点,根据设出顶点坐标公式y=a(x-4)2+3,求出a,然后令y=0,解得x.
解答:解:能.
∵OC=4,CD=3,
∴顶点D坐标为(4,3),
设y=a(x-4)2+3,
把A
代入上式,得
=a(0-4)2+3,
∴a=-
,
∴y=-
(x-4)2+3,
即y=-
x2+
x+
,
令y=0,得-
x2+
x+
=0,
∴x1=10,x2=-2(舍去).
故该运动员的成绩为10m.
∵OC=4,CD=3,
∴顶点D坐标为(4,3),
设y=a(x-4)2+3,
把A
| 5 |
| 3 |
| 5 |
| 3 |
∴a=-
| 1 |
| 12 |
∴y=-
| 1 |
| 12 |
即y=-
| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
令y=0,得-
| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
∴x1=10,x2=-2(舍去).
故该运动员的成绩为10m.
点评:本题主要考查二次函数的应用,由图形求出二次函数解析式,运用二次函数解决实际问题,比较简单.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
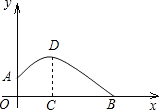 如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约
如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约 .铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
.铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
 .铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
.铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
 .铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
.铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?