Question

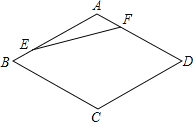
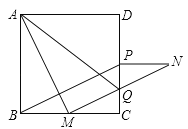
【题目】如图，正方形中，点是边上的任一点，连接并将线段绕点顺时针旋转得到线段，在边上取点使，连接.

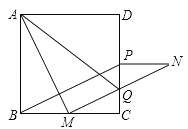
（1）求证：四边形是平行四边形；

（2）线段与交于点，连接，若，则与存在怎样的数量关系？请说明理由.

Answer 1

【答案】（1）见解析；（2）BM=MC．理由见解析.

【解析】

（1）根据正方形的性质可得AB=BC，∠ABC=∠C，然后利用“边角边”证明△ABM和△BCP全等；根据全等三角形对应边相等可得AM=BP，∠BAM=∠CBP，再求出AM⊥BP，从而得到MN∥BP，然后根据一组对边平行且相等的四边形是平行四边形证明即可；
（2）根据同角的余角相等求出∠BAM=∠CMQ，然后得出△ABM和△MCQ相似，根据相似三角形对应边成比例可得，再证得△AMQ∽△ABM，根据相似三角形对应边成比例可得，从而得到，即可得解．

解：（1）如图，

在正方形ABCD中，AB=BC，∠ABC=∠C=90°，
在△ABM和△BCP中，

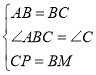
∴△ABM≌△BCP（SAS）．
∴AM=BP，∠BAM=∠CBP，
∵∠BAM+∠AMB=90°，
∴∠CBP+∠AMB=90°，
∴AM⊥BP，
∵AM并将线段AM绕M顺时针旋转90°得到线段MN，
∴AM⊥MN，且AM=MN
∴MN∥BP，MN =BP
∴四边形BMNP是平行四边形；

（2）BM=MC．理由如下：

∵∠BAM+∠AMB=90°，∠AMB+∠CMQ=90°，
∴∠BAM=∠CMQ，
又∵∠ABC=∠C=90°，
∴△ABM∽△MCQ，

∵△MCQ∽△AMQ，
∴△AMQ∽△ABM，

∴BM=MC．