题目内容
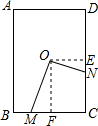
如图,O为矩形ABCD的中心,M为BC边上任一点,ON⊥OM且与CD边交于点N.若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为______.


如图,作OF⊥BC于F,OE⊥CD于E,
∵ABCD为矩形
∴∠C=90°
∵OF⊥BC,OE⊥CD
∴∠EOF=90°
∴∠EON+∠FON=90°
∵ON⊥OM
∴∠EON=∠FOM
∴△OEN∽△OFM
∴
=
∵O为中心
∴
=
=
=
∴
=
即y=
x
∵ABCD为矩形
∴∠C=90°
∵OF⊥BC,OE⊥CD
∴∠EOF=90°
∴∠EON+∠FON=90°
∵ON⊥OM
∴∠EON=∠FOM
∴△OEN∽△OFM
∴
| OE |
| OF |
| ON |
| OM |
∵O为中心
∴
| OF |
| OE |
| AB |
| AD |
| 6 |
| 4 |
| 3 |
| 2 |
∴
| OM |
| ON |
| 3 |
| 2 |
即y=
| 2 |
| 3 |


练习册系列答案
相关题目





