题目内容
(1)方程组 ,当k 时,有两个实数解.
,当k 时,有两个实数解.(2)已知
 是方程组
是方程组 的解,则m= ,n= .
的解,则m= ,n= .
【答案】分析:(1)先消去y得到关于x的一元二次方程,再令△>0,可求得k的范围;
(2)直接把x=2,y=-1代入方程组可得m、n的值.
解答:解:(1)
由(2)得y=4x+k,代入(1)得2x2-8x-k-1=0.
∵原方程组有两个实数解,则x要有两个不同的值,即方程2x2-8x-k-1=0有两个不相等实数解,
则△=(-8)2+4×2×(k+1)=64+8k+8=72+8k>0,
∴k>-9.
(2)把 代入方程组,得
代入方程组,得 ,
,
解得m=2,n=1.
故答案为>-9;2,1.
点评:本题考查了一元二次方程根的判别式,当△>0时,方程有两个不相等的实数根.此题要把方程组的解的问题转化为一元二次方程解的问题.同时考查了方程的解的含义.
(2)直接把x=2,y=-1代入方程组可得m、n的值.
解答:解:(1)

由(2)得y=4x+k,代入(1)得2x2-8x-k-1=0.
∵原方程组有两个实数解,则x要有两个不同的值,即方程2x2-8x-k-1=0有两个不相等实数解,
则△=(-8)2+4×2×(k+1)=64+8k+8=72+8k>0,
∴k>-9.
(2)把
 代入方程组,得
代入方程组,得 ,
,解得m=2,n=1.
故答案为>-9;2,1.
点评:本题考查了一元二次方程根的判别式,当△>0时,方程有两个不相等的实数根.此题要把方程组的解的问题转化为一元二次方程解的问题.同时考查了方程的解的含义.

练习册系列答案
相关题目
 ,当x=-4时,求k的值.
,当x=-4时,求k的值.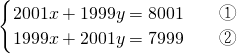
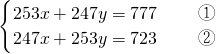 .
. ,当m为何值时,x>y?
,当m为何值时,x>y?