题目内容
 如图所示,∠1=∠2,P为BN上一点,且PD⊥BC于点D.AB+BC=2BD,则
如图所示,∠1=∠2,P为BN上一点,且PD⊥BC于点D.AB+BC=2BD,则
∠BAP+∠BCP=________度.
180
分析:过点P作PE⊥AB于E,根据角平分线上的点到角的两边的距离相等可得PD=PE,再利用“HL”证明△BPE和△BPD全等,根据全等三角形对应边相等可得BE=BD,然后求出AE=CD,再利用“边角边”证明△APE和△CPD全等,根据全等三角形对应角相等可得∠BCP=∠PAE,然后根据邻补角的定义解答即可.
解答: 解:如图,过点P作PE⊥AB于E,
解:如图,过点P作PE⊥AB于E,
∵∠1=∠2,PD⊥BC,
∴PD=PE,
在△BPE和△BPD中, ,
,
∴△BPE≌△BPD(HL),
∴BE=BD,
∵AB+BC=2BD,
∴BE-AE+BD+CD=2BD,
∴AE=CD,
在△APE和△CPD中, ,
,
∴△APE≌△CPD(SAS),
∴∠BCP=∠PAE,
∵∠BAP+∠PAE=180°,
∴∠BAP+∠BCP=180°.
故答案为:180.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,作辅助线构造出全等三角形的并二次证明全等是解题的关键.
分析:过点P作PE⊥AB于E,根据角平分线上的点到角的两边的距离相等可得PD=PE,再利用“HL”证明△BPE和△BPD全等,根据全等三角形对应边相等可得BE=BD,然后求出AE=CD,再利用“边角边”证明△APE和△CPD全等,根据全等三角形对应角相等可得∠BCP=∠PAE,然后根据邻补角的定义解答即可.
解答:
 解:如图,过点P作PE⊥AB于E,
解:如图,过点P作PE⊥AB于E,∵∠1=∠2,PD⊥BC,
∴PD=PE,
在△BPE和△BPD中,
 ,
,∴△BPE≌△BPD(HL),
∴BE=BD,
∵AB+BC=2BD,
∴BE-AE+BD+CD=2BD,
∴AE=CD,
在△APE和△CPD中,
 ,
,∴△APE≌△CPD(SAS),
∴∠BCP=∠PAE,
∵∠BAP+∠PAE=180°,
∴∠BAP+∠BCP=180°.
故答案为:180.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,作辅助线构造出全等三角形的并二次证明全等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
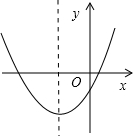 二次函数y=mx2+(6-2m)x+m-3的图象如图所示,则m的取值范围是( )
二次函数y=mx2+(6-2m)x+m-3的图象如图所示,则m的取值范围是( )| A、m>3 | B、m<3 | C、0≤m≤3 | D、0<m<3 |

 12、小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )
12、小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( ) 24、如图所示,向平静的水面投入一枚石子,在水面会激起一圈圈圆形涟漪,当半径从2cm变成5cm时,圆形的面积从
24、如图所示,向平静的水面投入一枚石子,在水面会激起一圈圈圆形涟漪,当半径从2cm变成5cm时,圆形的面积从 4、已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )
4、已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )