Question

【题目】如图，中，，，，点从点出发沿路径向终点运动，终点为点，点从点出发沿路径向终点运动，终点为点，点和分别以每秒和的运动速度同时开始运动，两点都要到达相应的终点时才能停止运动，分别过和作于，于.设运动时间为秒，要使以点，，为顶点的三角形与以点，，为顶点的三角形全等，则的值为______.

Answer 1

【答案】或7或8

【解析】

易证∠MEC＝∠CFN，∠MCE＝∠CNF．只需MC＝NC，就可得到△MEC与△CFN全等，然后只需根据点M和点N不同位置进行分类讨论即可解决问题．

①当0≤t＜4时，点M在AC上，点N在BC上，如图①，

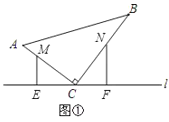
此时有AM＝2t，BN＝3t，AC＝8，BC＝15．

当MC＝NC即82t＝153t时全等，

解得t＝7，不合题意舍去；

②当4≤t＜5时，点M在BC上，点N也在BC上，如图②，

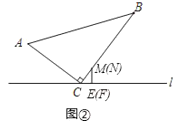
若MC＝NC，则点M与点N重合，即2t8＝153t，

解得t＝；

当5≤t＜时，点M在BC上，点N在AC上，如图③，

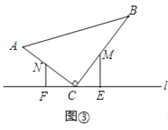
当MC＝NC即2t8＝3t15时全等，

解得t＝7；

④当≤t＜时，点N停在点A处，点M在BC上，如图④，

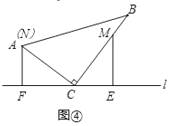
当MC＝NC即2t8＝8，

解得t＝8；

综上所述：当t等于或7或8秒时，以点M，E，C为顶点的三角形与以点N，F，C为顶点的三角形全等．

故答案为：或7或8．