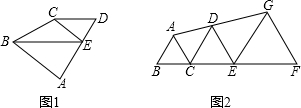题目内容

如图1，在四边形ABCD中，DC‖AB，AD=BC, BD平分∠ABC．

（1）求证：AD=DC；

（2）如图2，在上述条件下，若∠A=∠ABC= 60O，过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF．判断△DEF的形状并证明你的结论．

                 

 


证明:（1）因为DC‖AB，∠ CDB＝∠ABD, (1分)，又因为BD平分∠ABC，

所以∠ CBD＝∠ABD.（2分），∴∠CDB＝∠CBD, ∴BC=DC（3分），又AD=BC

∴AD=DC（4分）

（2）△DEF为等边三角形.（5分）

证明：∵BC=DC（已证），CF⊥BD，∴点F是BD的中点，∵∠DEB=90 O，∴EF=DF=BF．（6分）∵∠ABC= 60O，BD平分∠ABC，∠DFB=60 O，∴△DEF为等边三角形.（7分）

练习册系列答案
相关题目
（1）已知：如图1，在四边形ABCD中，E是AD上一点，EC∥AB，EB∥CD，若S△DEC=1，S△ABE=3，则S△BCE=
 
；若S△DEC=S1，S△ABE=S2，S△BCE=S，请直接写出S与S1、S2间的关系式：
 
；
（2）如图2，△ABC、△DCE、△GEF都是等边三角形，且A、D、G在同一直线上，B、C、E、F也在同一直线上，S△ABC=4，S△DCE=9，试利用（1）中的结论得△GEF的面积为
 
．
精英家教网
我们把既有外接圆又有内切圆的四边形称为双圆四边形，如图1，四边形ABCD是双圆四边形，其外心为O1，内心为O2．
（1）在平行四边形、矩形、菱形、正方形、等腰梯形中，双圆四边形有
 
个；
（2）如图2，在四边形ABCD中，已知：∠B=∠D=90°，AB=AD，问：这个四边形是否是双圆四边形？如果是，请给出证明；如果不是，请说明理由；
（3）如图3，如果双圆四边形ABCD的外心与内心重合于点O，试判定这个四边形的形状，并说明理由．
精英家教网
（2012•黑河）如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN
（1）如图2，在梯形ABCD中，BC∥AD，AB=BC=CD，点M、N分别在AD、CD上，若∠MBN=
1
2
∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．
（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN=
1
2
∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明．
（2013•咸宁）阅读理解：
如图1，在四边形ABCD的边AB上任取一点E（点E不与点A、点B重合），分别连接ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．解决问题：
（1）如图1，∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；
（2）如图2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD的边AB上的一个强相似点E；
拓展探究：
（3）如图3，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB和BC的数量关系．
（2011•东台市二模）在四边形ABCD中，AC=AB，DC=DB，∠CAB=60°，∠CDB=120°，E是AC上一点，F是AB延长线上一点，且CE=BF．

思考验证：
（1）求证：DE=DF；
（2）在图1中，若G在AB上且∠EDG=60°，试猜想CE、EG、BG之间的数量关系并证明；
归纳结论：
（3）若题中条件“∠CAB=60°且∠CDB=120°”改为∠CAB=α，∠CDB=180°-α，G在AB上，∠EDG满足什么条件时，（2）中结论仍然成立？（只写结果不要证明）
探究应用：
（4）运用（1）（2）（3）解答中所积累的经验和知识，完成下题：如图2，在四边形ABCD中，∠ABC=90°，∠CAB=∠CAD=30°，E在AB上，DE⊥AB，且∠DCE=60°，若AE=3，求BE的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网