题目内容
如图所示,直线AB、CD相交于点P,点Q、E在AB上,已知:PQ=8,QE=3,sin∠BPC= ,O为射线QA上的一动点,⊙O的半径为
,O为射线QA上的一动点,⊙O的半径为 ,开始时,O点与Q点重合,⊙O沿射线QA方向移动.
,开始时,O点与Q点重合,⊙O沿射线QA方向移动.
(1)当圆心O运动到与点E重合时,判断此时⊙O与直线CD的位置关系,交说明你的理由;
(2)设移动后⊙O与直线CD交于点M、N,若△OMN是直角三角形,求圆心O移动的距离.

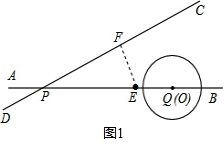 解:(1)如图1,过点E作EF⊥CD于点F,
解:(1)如图1,过点E作EF⊥CD于点F,∵PQ=8,QE=3,
∴PE=PQ-QE=8-3=5,
∵sin∠BPC=
 ,
,∴EF=PE•sin∠BPC=5×
 =
= ,
,∴此时⊙O与直线CD相切;
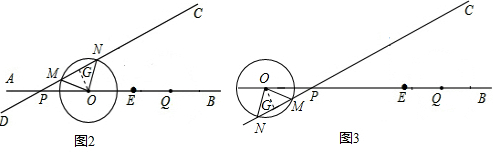
(2)如图2,当O点在P点的右侧时:过点O作OG⊥CD于点G,
∵△OMN是直角三角形,OM=ON=
 ,
,∴2OG2=OM2,即OG=
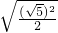 =
= ,
,∵sin∠BPC=
 ,
,∴OP=
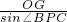 =
=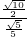 =
= .
.∴OQ=PQ-OP=8-
 .
.如图3,当点O在点P的左侧时,同理可得OP=
 ,
,∴OQ=PQ+OP=8+

答:圆心O移动的距离是8-
 或8+
或8+ .
.
分析:(1)过点E作EF⊥CD于点F,求出PE的长,根据sin∠BPC=
 即可求出EF的长,进而可判断出⊙O与直线CD的位置关系;
即可求出EF的长,进而可判断出⊙O与直线CD的位置关系;(2)过点O作OG⊥CD于点G,由勾股定理求出OG的长,再根据sin∠BPC=
 即可求出OP的长,进而可得出结论.
即可求出OP的长,进而可得出结论.点评:本题考查的是直线与圆的位置关系及锐角三角函数的定义,熟知直线与圆的三种位置关系是解答此题的关键.

练习册系列答案
相关题目
 12、如图所示,直线AB、CD相交于点O.若OM=ON=MN,那么∠APQ+∠CQP=
12、如图所示,直线AB、CD相交于点O.若OM=ON=MN,那么∠APQ+∠CQP= 24、如图所示,直线AB与x轴交于A,与y轴交于B.
24、如图所示,直线AB与x轴交于A,与y轴交于B. 如图所示,直线AB与CD相交于点O,∠DOE=60°,∠BOE=27°,求∠BOD,∠AOD,∠AOC的度数.
如图所示,直线AB与CD相交于点O,∠DOE=60°,∠BOE=27°,求∠BOD,∠AOD,∠AOC的度数. 如图所示,直线AB、CD相交于点O,∠BOD=40°,OA平分∠EOC,则∠EOD的度数为
如图所示,直线AB、CD相交于点O,∠BOD=40°,OA平分∠EOC,则∠EOD的度数为 如图所示,直线AB、CD、EF相交于点O,且EF⊥CD,若∠AOE=30°,则∠AOC=
如图所示,直线AB、CD、EF相交于点O,且EF⊥CD,若∠AOE=30°,则∠AOC=