Question

如图，AB是⊙O的直径，点F，C是⊙O上两点，且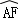==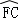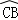，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．

（1）求证：CD是⊙O的切线；

（2）若CD=2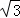，求⊙O的半径．

Answer 1

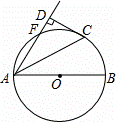
（1）证明：连结OC，如图，

∵=，

∴∠FAC=∠BAC，

∵OA=OC，

∴∠OAC=∠OCA，

∴∠FAC=∠OCA，

∴OC∥AF，

∵CD⊥AF，

∴OC⊥CD，

∴CD是⊙O的切线；

（2）解：连结BC，如图，

∵AB为直径，

∴∠ACB=90°，

∵==，

∴∠BOC=×180°=60°，

∴∠BAC=30°，

∴∠DAC=30°，

在Rt△ADC中，CD=2，

∴AC=2CD=4，

在Rt△ACB中，BC=AC=×4=4，

∴AB=2BC=4，

∴⊙O的半径为4．