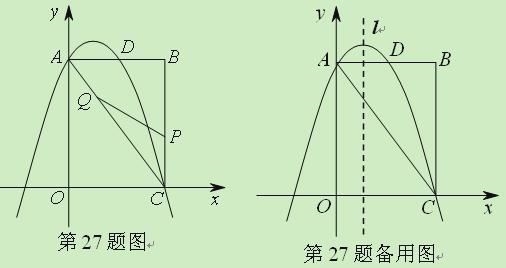
��Ŀ����
����Ŀ����ͼ��������y��ax2+bx+2��a��0����x�ύ�ڵ�A����1��0���͵�B��2��0������y�ύ�ڵ�C��
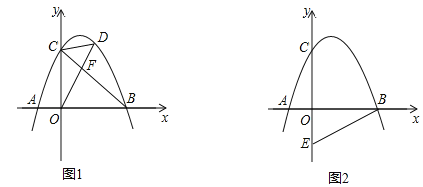
��1����������ߵĺ�������ʽ��
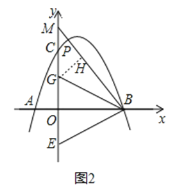
��2����ͼ1������BC����D��ֱ��BC�Ϸ��������ϵĵ㣬����OD��CD��OD��BC�ڵ�F����S��COF��S��CDF��2��1ʱ�����D�����ꣻ
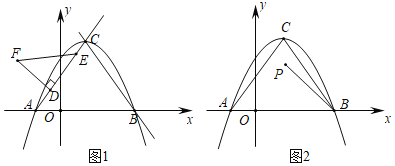
��3����ͼ2����E������Ϊ��0����1���������������Ƿ���ڵ�P��ʹ��OBP��2��OBE�������ڣ���ֱ��д�����������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+x+2����2��D��1��2������3����![]() ����
����![]() ����
����
��������
��1�����ô���ϵ���������ʽ���ɵõ��𰸣�
��2������D��DH��y�ύBC�ڵ�H����x���ڵ�G������S��COF��S��CDF��2��1�õ�OF��DF��2��1���������������ε����ʿɵô𰸣�
��3����������ۣ��ٵ���P��x���Ϸ�ʱ����y����ȡ��G��1��0��������BG�����OBG����OBE������B��ֱ��PB���������ڵ�P����y���ڵ�M��ʹ��GBM����GBO�����OBP��2��OBE��Ȼ�����![]() �Ľ���ʽ��������������⼴�ɣ�
�Ľ���ʽ��������������⼴�ɣ�
�ڵ���P��x���·�ʱ������M��0��![]() ������x��ĶԳƵ�N��0��
������x��ĶԳƵ�N��0��![]() �������
�������![]() �Ľ���ʽ��������������⼴�ɣ�
�Ľ���ʽ��������������⼴�ɣ�
�⣺��1����A����1��0����B��2��0����
���A����1��0����B��2��0������y��ax2+bx+2�ã�
![]()
��ã�![]()
��������ߵĺ�������ʽΪy����x2+x+2��
��2����ͼ1������D��DH��y�ύBC�ڵ�H����x���ڵ�G��
��������y����x2+x+2��y�ύ�ڵ�C��
��C��0��2����
��ֱ��BC����ʽΪy��kx+b��
��![]() ���
���![]()
��ֱ��BC����ʽΪy����x+2��
��S��COF��S��CDF��2��1��
��OF��DF��2��1��
��DH��OC��
���OFC�ס�DFH��
��![]()
��OC��2DH��
��D��a����a2+a+2������H��a����a+2����
��DH����a2+a+2������a+2������a2+2a��
��2��2����a2+2a����
���a��1��
��D��1��2����
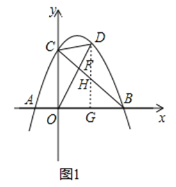
��3���ٵ���P��x���Ϸ�ʱ��
��y����ȡ��G��1��0��������BG�����OBG����OBE������B��ֱ��PB���������ڵ�P����y���ڵ�M��ʹ��GBM����GBO��
���OBP��2��OBE��
����G��GH��BM��
��E��0����1����
��OE��OG��GH��1��
��MH��x����MG��![]() ��
��
��Rt��OBM��OB2+OM2��MB2��
�ࣨ![]() +1��2+4����x+2��2��
+1��2+4����x+2��2��
��ã�x��![]() ��
��![]() ����ȥ��
����ȥ��
��MG��![]() ��
��![]()
��OM��OG+MG��![]()
���M��0��![]() ����
����
����B��2��0����M��0��![]() �����������һ�κ�������ʽy��mx+n��
�����������һ�κ�������ʽy��mx+n��
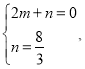
��ã�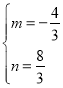 ��
��
��ֱ��BM�ı���ʽΪ��![]()
��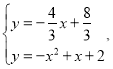
��ã�![]() ��x��2����ȥ����
��x��2����ȥ����
���P![]() ��
��
�ڵ���P��x���·�ʱ��
����M��0��![]() ������x��ĶԳƵ�N��0��
������x��ĶԳƵ�N��0��![]() ����
����
ͬ���ɵã�
ֱ��BN�Ľ���ʽΪ![]()
��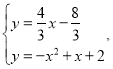
��ã�![]() ��x��2����ȥ����
��x��2����ȥ����
���P![]() ��
��
�ۺ����Ͽɵã���P������Ϊ![]() ��
��![]() ��
��