题目内容
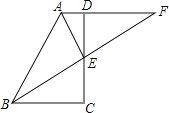
【题目】如图,已知反比例函数![]() 的图像与一正比例函数的图像相交于点
的图像与一正比例函数的图像相交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求正比例函数的解析式;
(2)若正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像在第一象限内交于点
的图像在第一象限内交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,且交直线
为垂足,且交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,求梯形
为垂足,求梯形![]() 的面积;
的面积;
(3)连结![]() ,求
,求![]() 的面积.
的面积.

【答案】(1)正比例函数的解析式为![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据自变量的值,可得相应的函数值,根据待定系数法,可得函数解析式;(2)根据自变量的值求得相应的函数值,即点P的坐标,通过联立两个解析式得方程组求交点B的坐标,求得线段BD,CD的长,根据梯形面积公式求解;(3)根据反比例函数的性质可得![]() ,利用割补法求得三角形的面积.
,利用割补法求得三角形的面积.
(1)设正比例函数的解析式为:![]() ,
,
把![]() 代入
代入![]() ,
,
![]() ,
,
∴A(1,4)
把![]() 代入
代入![]() 得,得
得,得![]() ,
,
∴正比例函数的解析式为:![]()
(2)把![]() 代入
代入![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
联立![]() 与反比例函数
与反比例函数![]() 得,
得,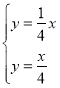 ,
,
解得:![]() 或
或![]() ,
,
即![]() ,
,
![]() ,
,![]() ,
,
![]()
(3)∵A,B在双曲线![]() 上,且AC⊥x轴,BD⊥x轴,
上,且AC⊥x轴,BD⊥x轴,
∴![]()
∴![]()

练习册系列答案
相关题目