Question

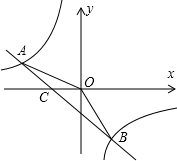已知点A（-8，n），B（3，-8）是一次函效y=kx+b的图象和反比例函数y=

m

x

图象的两个交点．
（1）求反比例函数和一次函数的解析式；
（2）求直线AB与x轴的交点C的坐标及△AOB的面积；
（3）求不等式kx+b-

m

x

＞0的解集（请直接写出答案）．

Answer 1

分析：（1）先把B（3，-8）代入反比例函数y=

m

x

得m=-8×3=-24，则确定反比例函数的解析式为y=-

24

x

，再把A（-8，n）代入y=-

24

x

，可确定A点坐标为（-8，3），然后利用待定系数法可求出一次函数的解析式；
（2）对于y=-x-5，令y=0，则-x-5=0，解得x=-5，可确定C点坐标为（-5，0），然后利用S_△AOB=S_△AOC+S_△BOC进行计算即可；
（3）观察函数图象得到当x＜-8或0＜x＜3时，一次函数图象都在反比例函数图象上方，即有kx+b-

m

x

＞0．

解答：解：（1）把B（3，-8）代入反比例函数y=

m

x

得m=-8×3=-24，
∴反比例函数的解析式为y=-

24

x

，
把A（-8，n）代入y=-

24

x

得-8n=-24，解得n=3，
∴A点坐标为（-8，3），
把A（-8，3），B（3，-8）代入一次函数y=kx+b，
得

-8k+b=3 3k+b=-8

，
解得

k=-1 b=-5

，
∴一次函数的解析式为y=-x-5；

（2）对于y=-x-5，令y=0，则-x-5=0，解得x=-5，
∴C点坐标为（-5，0），
∴S_△AOB=S_△AOC+S_△BOC=

1

2

×5×3+

1

2

×5×8=27.5；

（3）x＜-8或0＜x＜3．

点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数的交点坐标同时满足两个函数的解析式．也考查了待定系数法求函数的解析式以及观察函数图象的能力．