题目内容
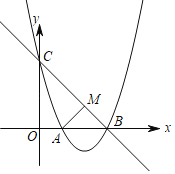
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)如图2,若点![]() 是直线
是直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,当点
,当点![]() 的横坐标为
的横坐标为![]() 时,求
时,求![]() 的面积;
的面积;
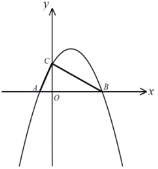
(3)若点![]() 为抛物线上的一个动点,以点
为抛物线上的一个动点,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,当
,当![]() 在运动过程中与直线
在运动过程中与直线![]() 相切时,求点
相切时,求点![]() 的坐标(请直接写出答案).
的坐标(请直接写出答案).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 为
为![]() 或
或![]()
【解析】
⑴根据![]() ,
,![]() 求出B、C的坐标,再代入求出解析式;
求出B、C的坐标,再代入求出解析式;
⑵根据题意可证△PED∽△BOC,再利用相似三角形的面积比等于相似比的平方求出△PED的面积;
⑶根据二次函数图象的性质及切线性质构造相似三角形来求出点M的坐标.点M在直线BC的上方或在直线BC的下方两种情况来讨论.
解:(1)![]() ,
,![]()
![]() ,
,![]() ,
,
![]() 点
点![]() 为
为![]() ,点
,点![]() 为
为![]()
代入![]() 得:
得:
![]() ,
,![]()
![]()
(2)当![]() 时,
时,![]() ,
,![]() 点
点![]() 坐标为
坐标为![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]()
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
![]() 平行于
平行于![]() 轴,
轴,![]() 点
点![]() 坐标为
坐标为![]()
![]()
![]() 平行于
平行于![]() 轴,
轴,![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() 与
与![]() 的面积之比是对应边
的面积之比是对应边![]() 与
与![]() 的平方,
的平方,
![]() 的面积为
的面积为![]() ,
,
![]() 的面积是
的面积是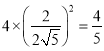
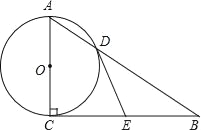
(3)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
![]() ,
,![]()
![]() 与直线
与直线![]() 相切,
相切,![]() ,
,![]()
设点![]() 的坐标为
的坐标为![]()
如图1,点![]() 的坐标为
的坐标为![]()
代入直线![]() 得
得
![]()
解得![]() ,
,![]()
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]()
图1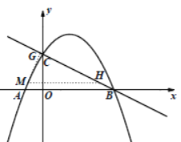
如图2,点![]() 的坐标为
的坐标为![]()
代入直线![]() 得
得
![]()
方程无解
综上,点![]() 为
为![]() 或
或![]()
图2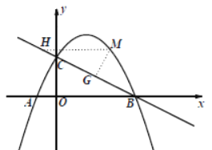

练习册系列答案
相关题目