题目内容
如图，已知?ABCD中AC=AD，∠B=72°，则∠CAD=________°．
36
分析：易得∠D=∠B，由AC=AD可得∠ACD=∠D，根据三角形的内角和是180°可得∠CAD的度数．
解答：∵四边形ABCD是平行四边形，
∴∠D=∠B=72°，
∵AC=AD，
∴∠ACD=∠D=72°，
∴∠CAD=180°-∠ACD-∠D=36°．
故答案为：36．
点评：本题考查了平行四边形的性质，用到的知识点为：平行四边形的对角相等；等边对等角；三角形的内角和是180°．
分析：易得∠D=∠B，由AC=AD可得∠ACD=∠D，根据三角形的内角和是180°可得∠CAD的度数．
解答：∵四边形ABCD是平行四边形，
∴∠D=∠B=72°，
∵AC=AD，
∴∠ACD=∠D=72°，
∴∠CAD=180°-∠ACD-∠D=36°．
故答案为：36．
点评：本题考查了平行四边形的性质，用到的知识点为：平行四边形的对角相等；等边对等角；三角形的内角和是180°．
练习册系列答案
名校课堂系列答案
相关题目
14、如图，已知?ABCD中，AB=4，BC=6，BC边上的高AE=2，则DC边上的高AF的长是
26、如图，已知?ABCD，AE平分∠BAD，交DC于E，DF⊥BC于F，交AE于G，且DF=AD．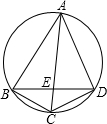
如图，已知ABCD是圆的内接四边形，对角线AC和BD相交于E，BC=CD=4，AE=6，如果线段BE和DE的长都是整数，则BD的长等于
如图，已知ABCD是圆O的内接四边形，AB=BD，BM⊥AC于M，求证：AM=DC+CM．