题目内容
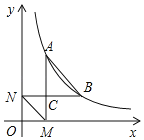
【题目】如图,点A、B在函数y=![]() (x>0,k>0且k是常数)的图象上,且点A在点B的左侧过点A作AM⊥x轴,垂足为M,过点B作BN⊥y轴,垂足为N,AM与BN的交点为C,连结AB、MN.若△CMN和△ABC的面积分别为1和4,则k的值为( )
(x>0,k>0且k是常数)的图象上,且点A在点B的左侧过点A作AM⊥x轴,垂足为M,过点B作BN⊥y轴,垂足为N,AM与BN的交点为C,连结AB、MN.若△CMN和△ABC的面积分别为1和4,则k的值为( )
A.4B.4![]() C.
C.![]() D.6
D.6
【答案】D
【解析】
依题意可分别设M(a,0),N(0,b),由△CMN的面积可得ab的值,利用反比例函数图象上点的坐标特征可得A (a,![]() ),B(
),B(![]() ,b),再由△ABC的面积可列出方程,结合ab的值可求出k.
,b),再由△ABC的面积可列出方程,结合ab的值可求出k.
解:设点M(a,0),N(0,b)
∵AM⊥x轴,且点A在反比例函数y=![]() (x>0,k>0且k是常数)的图象上,
(x>0,k>0且k是常数)的图象上,
∴点A的坐标为(a,![]() ),
),
BN⊥y轴,同理可得:B(![]() ,b)
,b)
则点C(a,b)
S△CMN=![]() =
=![]() ab=1
ab=1
∴ab=2
∵AC=![]() ,BC=
,BC=![]()
![]() =
=![]() =4
=4
即![]() ,且ab=2
,且ab=2
(k﹣2)2=16
解得:k=6,k=﹣2(舍去)
故选:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目