题目内容
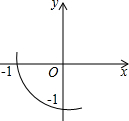如图，已知函数y=ax2+bx+c的图象过（-1，0）和（0，-1）两点，则a的取值范围是________．
0＜a＜1
分析：根据开口判断a的符号，根据与x轴，y轴的交点判断c的值以及b用a表示出的代数式．进而根据当x=1时，y＜0判断出a的范围．
解答：抛物线开口向上，a＞0，
图象过点（0，-1），c=-1，
图象过点（-1，0），a-b+c=0，
∴b=a-1，
由题意知，当x=1时，应有y＜0，
∴a+b+c＜0，
∴a+（a-1）-1＜0，
∴a＜1，
∴实数a的取值范围是0＜a＜1．
故答案为：0＜a＜1．
点评：难点是推断出当x=-1时，应有y＜0．有了c的值，判断a的值应用a表示出b，进而根据x=1或-1判断y的值，判断a的具体范围．
分析：根据开口判断a的符号，根据与x轴，y轴的交点判断c的值以及b用a表示出的代数式．进而根据当x=1时，y＜0判断出a的范围．
解答：抛物线开口向上，a＞0，
图象过点（0，-1），c=-1，
图象过点（-1，0），a-b+c=0，
∴b=a-1，
由题意知，当x=1时，应有y＜0，
∴a+b+c＜0，
∴a+（a-1）-1＜0，
∴a＜1，
∴实数a的取值范围是0＜a＜1．
故答案为：0＜a＜1．
点评：难点是推断出当x=-1时，应有y＜0．有了c的值，判断a的值应用a表示出b，进而根据x=1或-1判断y的值，判断a的具体范围．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，已知函数y1=kx+b与函数y2=| m |
| x |
| m |
| x |
| A、x1=1，x2=-3 |
| B、x1=-1，x2=3 |
| C、x1=1，x2=-1 |
| D、x1=3，x2=-3 |
14、如图，已知函数y=3x+b和y=ax-3的图象交于点P（-2，-5），则根据图象可得不等式3x+b＞ax-3的解集在数轴上表示正确的是（ ）
12、如图，已知函数y=x+b和y=ax+3的图象交点为P，则不等式x+b＞ax+3的解集为
如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于
如图，已知函数